Original title: "Paths toward single-slot finality》
Original title: "
Original author: Vitalik Buterin, founder of Ethereum
Compilation of the original text: Double Spending (@doublespending), ECN community volunteer
Special thanks to Justin Drake, Dankrad Feist, Alex Obadia, Hasu, Anders Elowsson, and fellow hackmd anonymous folks for their review and feedback on various versions of this article.
Currently, Ethereum blocks require between 64 and 95 slots (about 15 minutes) to achieve finality. This is reasonable and a compromise on the decentralization/finality time/overhead curve: 15 minutes is not too long, and comparable to confirmation times of existing exchanges, allowing users to Even though there are a large number of validators because the deposit size is 32 ETH (instead of the 1500 ETH required to pledge in the early stage).However, there are still good reasons for reducing the finality time toa slot
. This is a research status review reviewing the roadmap to achieve this goal.
The current operation mode and basis of Ethereum staking
Ethereum's LMD GHOST + Casper FFG consensus is a compromise between two mainstream consensus algorithms popular in proof-of-stake blockchains:Chain-based consensus algorithm:
Each slot (a preset time interval, such as 12 seconds in Ethereum) generates a message (block). Chain-based consensus algorithms maximize the number of participants and reduce chain load, but are prone to forks and do not have any notion of finality.Traditional BFT (Byzantine Fault Tolerance) consensus algorithm:
In each slot, except for a validator who generates a block, each validator will generate two messages ("attestation", translator's note: that is, "witness"), and the block of one slot will be in the next slot. Irreversible "finality" was achieved before the start. The traditional BFT consensus algorithm minimizes the time to achieve finality, but at the expense of high load on the chain and only supporting a small number of participants.
Unlike a purely chain-based system, the Ethereum consensus algorithm will perform thousands of witness votes on the chain head in parallel in each slot. Every epoch (32 slots, or 6.4 minutes), all active validators have the opportunity to witness (attest) once. Two epochs later, the Casper FFG finalizer finalizes the block, and since then, rolling back the block would require at least one-third of validators to burn their stake deposits: the cost of the attack would exceed 4 million ETH. This distinguishes it from a purely traditional BFT system where finalization is achieved after a slot.
Therefore, what Ethereum achieves today is:moderate finalization time
— Longer time compared to traditional BFT finalization in a single slot, but not weeks or months, or never offered like chain-based consensus algorithmsmoderate chain load
- Thousands of messages per slot, but less than hundreds of thousands of messages when using traditional BFTmoderate number of nodes
——Becoming a verifier requires a pledge of 32 ETH: Compared with the chain-based consensus algorithm, the threshold is higher. In the chain-based consensus algorithm, even a small amount of Token can participate in the consensus. A large number of Tokens are much lower than the threshold
Ethereum’s support for higher-strength chainloads is enabled by efficiency gains in BLS signature aggregation. Because of these efficiency gains, chainloads capable of high intensity (in terms of messages per second) can be translated into chainloads that require only moderate data and CPU overhead.
BLS signature aggregation works by aggregating multiple signatures into one, such that verifying the aggregated signature requires only one additional elliptic curve addition (not multiplication) per participant, and 64 bytes can accommodate any number of participants , while each participant only needs one extra bit to store.
The combination of the chain-based consensus algorithm and the traditional BFT consensus algorithm, coupled with the pure efficiency improvement derived from BLS, forms the current consensus algorithm of Ethereum.
So why change it?
In the years since the original Ethereum consensus protocol was developed using the above reasoning, we have had a major good news and a major bad news.
Bad News: Hybrid Consensus Mechanisms Actually Have Many Unavoidable Problems
The hybrid consensus mechanism combines fork selection rules and finality tools. The former is used to advance consensus slot by slot, and the latter is used to finalize blocks later. The biggest problem with the hybrid consensus mechanism is:
User Experience: Most users don't want to wait 15 minutes for a transaction to be finalized. Currently, even exchanges generally consider deposits to be "finalized" after 12 to 20 confirmations (about 3 to 5 minutes), although 12 to 20 PoW confirmations provide weak security guarantees (unlike real compared to PoS finalization).
MEV reorganization: Hybrid consensus mechanisms still retain the fact that short-term reorganizations are possible, thus opening the door for malicious validators with a near-majority or majority to conspire to reorganize the blockchain to extract MEV value. This article develops this argument in more detail.
Interaction flaws: The "interface" between the Casper FFG finalization and the LMD GHOST fork choice is a source of significant complexity, leading to many attacks that require fairly complex patches to fix, and more weaknesses are discovered from time to time.
Additional protocol complexity: Hundreds of lines of specification are used to maintain mechanisms such as validator set shuffle.
Good News: Very Large Validator Sets Are More Possible Than You Think Because of BLS Aggregation
The specific efficiencies achieved by BLS have improved by leaps and bounds over the past three years, while we have learned more about how to efficiently process and combine large volumes of messages and data.
Using BLS to support a large number of validators faces two major bottlenecks:
Final Verification: Verifying signatures from N verifiers requires up to N/2 ECADDs to compute the group public key and N bits (N/8 bytes) of bitfields to store participants. In practice, these numbers need to increase by as much as 16 times due to the redundant aggregators required for view-merge.
Aggregation: Combining the signatures sent by each of the N verifiers into an aggregate signature. This requires a total of at least 96*N bytes of bandwidth to process, and requires at least N ECADDs on top of the G2 group (more than 4 times computationally intensive), but is simpler to distribute across subnets.
In fact, the final validation scales very well. A single ECADD can be done in about 500 nanoseconds (ns), so 1 million ECADDs will take about 500 milliseconds (ms). The size of the 1 million validator bitfield is only 128 kB.
The redundancy of view-merge may require up to 16 individual signatures to be verified per slot; this raises the data storage requirements to a still manageable 2 MB (roughly equal to the size cap of blob data per block in EIP-4844, and the current upper limit of calldata size per block), while the worst-case ECADD operation cost increases by about 8 times (due to the clever precomputation trick, it does not need to increase by 16 times).
These are worst-case values; in the typical case, the bitfields of the 16 aggregators are roughly identical, allowing the major additional cost of multiple aggregations to be compressed.
Aggregation is more challenging, but quite doable. Recent research has greatly improved our understanding of how to aggregate large numbers of signatures within a single slot. The good news is that we have good reason to believe that processing hundreds of thousands of signatures per slot is possible, although further research work is still needed to identify and agree on the best solution.
The combination of these two facts means that the trade-off is no longer tilted towards a compromise between chain-based and BFT-based PoS, but a solution closer to the full traditional BFT route, that is, finalized before the start of the next block. per block.
What key issues do we need to address to achieve single slot finality?
There are three key questions:
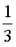Develop the exact consensus algorithm: We are less accepting of Tendermint or other existing BFT algorithms, because we value this very much: even at
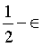In the case of validators offline, the blockchain can still be kept alive (this is not provided by traditional BFT). We need to add a fork choice rule, inactivity leak and recovery mechanism to enable this liveness. Ideally, we would have optimal security: when the network is synchronized, the fault tolerance rate is
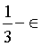。; When the network is not synchronized, the fault tolerance rate is
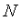Determine the optimal aggregation strategy. for the highest possible, we want to aggregate fromvalidator's signatures and pack them into a block, and the node overhead is a level we are willing to accept.
Determine the economic model of validators. Despite improvements in the two steps of aggregation and final verification, a single slot finalized Ethereum may eventually be able to support a theoretical upper limit on the number of validators that is smaller than the current Ethereum. If this number ends up being lower than the number of participating validators, how do we limit participation, and what sacrifices do we make?
What would the exact consensus algorithm look like?
As mentioned above, we want a consensus algorithm that follows the Casper FFG + LMD GHOST "finalization chain + optimistic chain" paradigm. Under extreme conditions, the optimistic chain can be rolled back, but the finalization chain can never be rolled back.
This requires a similar combination of fork choice rules and finality tools to existing consensus, with one key difference: currently, we typically run fork choice rules and finality tools concurrently, but in a single slot In a world of finality, we would either run the fork choice rule, or the finality tool: if less than
of validators are online and working honestly, run the former; otherwise, run the latter.
Specific proposals for this algorithm are still in progress; no formal results or papers have yet been published.
What are the problems in developing an optimal aggregation strategy?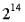
Let's first look at how aggregation is currently done. In a single slot, there are about
verifiers, which are divided into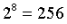
committees, each with approximately
verifiers. First, validators in each committee broadcast their signatures in a p2p subnet dedicated to that committee. There are 16 designated aggregators in each committee, and each aggregator combines all the signatures it sees into an aggregated signature (96 bytes + 256 bit fields). Designated aggregators publish their aggregated signatures to the main subnet.
The block proposer then picks the best (i.e., the largest total balance of participants) aggregated signature from each committee and packs it into the block. With patches for view merge fork selection, they also add a sidecar object containing signatures of other aggregates; this protects the view merge mechanism from malicious behavior as long as at least one aggregator in each committee is honest Aggregator influence.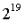
If we want to extend this model to a scenario where a single slot achieves finality, then we need to be able to process all
(or however many we have) validators. This requires one of two trade-offs:
Increase the number of validators for a single committee or increase the number of committees, or both, to accommodate more validators.
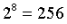Move to a three-tier aggregation, two-tier committee structure. First, the signature is divided into
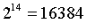Groups of are aggregated, then the size is
groups, and finally the full set of validators.
The former requires greater p2p network bandwidth, the latter requires higher latency, and more p2p subnet levels bring higher risk and additional complexity to ensure that view merge is not affected by malicious aggregators in all levels .
Analytical research on these two strategies is ongoing.
What are the problems with the validator economic model?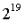Currently, Ethereum has about
active validators (445,064 at the time of writing, to be precise), each with 32 ETH staked. By the time single slot finality is achieved, the number of validators may increase to
or even higher.
This brings up a major problem: if we can only process signatures from N validators per slot, but if more than N validators want to participate, how do we determine who goes and who stays?
This is a significant issue, as any solution would involve weakening one or more features of the staking system that are considered security guarantees.
Good News: Benefits from Supporting Spontaneous Validator Balance Consolidation
Because single slot finality removes the concept of committees (and even danksharding doesn't use fixed-size committees), we no longer need a validator effective balance cap of 32 ETH. Considering the stability of the p2p network, we still want a higher upper limit (eg, 2048 ETH), but even this means that a large number of validator slots that would otherwise belong to rich users will be merged into a small number More validator slots.
We can use Zipf's law to estimate the payoff of integrating validator slots with wealthy users: the number of stakers with a given balance is inversely proportional to their balance (so the number of stakers with a balance of 100-2000 ETH is equal to the number of stakers with a balance of 1000-2000 ETH 10 times the number of participants).
Using early historical data from the beacon chain, Zipf's law seems to fit the distribution fairly accurately: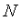Assuming that Zipf's law is followed,
stakers will have approximately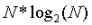
ETH, then need today
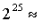validator slots. Bundle
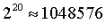Filling in this formula with 33.5 million ETH, we can get a total of 65,536 pledgers, and today’s Ethereum needs to consume
validator slots. Thus, removing the effective balance cap entirely reduces the number of validator slots that need to be processed to 65536, while maintaining the cap of 2048 ETH (up from the current 32 ETH) would only add about 1000 to 2000 additional validators. Just ~2x the aggregate performance or ~2x the load to be able to handle single slot finality in the current case!
As a side benefit, this is also fairer to small stakers who can stake their entire balance rather than a portion (e.g. someone who currently owns 48 ETH can only stake 2/3 of their ETH). Staking rewards are automatically re-staked, allowing even small validators to benefit from compounding. In fact, it might even be a good idea to raise the staking cap to 2048 ETH for this very reason!
However, we still need to deal with exceptions: (i) the distribution of validator balances no longer follows Zipf's law, or (ii) wealthy validators do not intend to consolidate their balances, or (iii) stake more than 33 million ETH.
I thought of two realistic strategies for dealing with these situations: Supercommittee and capping the validator set size.
Idea 1: Super Committee
Not all validators participate in each round of Casper FFG, but only a medium-sized super committee composed of tens of thousands of people participates, so that each round of consensus occurs within a slot.
This technical idea was first introduced in this post. This post describes the idea in more detail, but the core principle is simple: at any given time, only one medium-sized supercommittee (e.g., worth 4 million ETH) is active, randomly sampled from the full set of validators . Every time the chain reaches finality, the committee changes, with up to 25% of its members being replaced by a random sample of new validators.
In this strategy, "Who stays and who goes?" is: Everyone will stay part of the time and leave another part of the time.
How big does the supercommittee have to be?
This question boils down to a simpler question: how much would it cost to 51% attack Ethereum? Ideally, the amount of ETH slashed due to the attack and penalty for sabotage needs to be greater than the actual gain from the attack. The cost of an attack should even be high enough to deter or cost a powerful attacker with a strong external motivation to destroy the chain.
Answering the question of how much ETH is needed to achieve this goal inevitably relies on intuition. Here are some questions we can ask:
Suppose Ethereum is 51% attacked, it takes a few days for the community to coordinate off-chain governance to recover, and X% of ETH is burned. How large does X need to be to have a net benefit to the Ethereum ecosystem?
Suppose a large exchange is hacked resulting in the loss of millions of ETH, the attacker deposits the proceeds and takes over 51% of the validators. How many times can an attacker perform a 51% attack on the chain before the stolen funds are completely destroyed?
Estimates from Justin Drake suggest that the current cost of a spawn-camp attack on Bitcoin (that is, a 51% attack that continues until the community changes the PoW algorithm) is about $10 billion, or 1% of Bitcoin's market value. How many times that should the cost of a 51% attack on Ethereum be?
image description
An internal vote by Ethereum researchers
If we only focus on 51% attacks that do not rely on network latency, an attack cost of 1 million ETH means a supercommittee of 2 million ETH size (approximately 65,536 validators). If we also consider a 34% attack involving a complex combination of malicious validators and network manipulation, the scale is 3 million ETH (approximately 97,152 validators).
complexity cost
In addition to reducing attack costs, another major weakness of this scheme is complexity, including protocol complexity and analysis complexity. in particular:
We need hundreds of lines of specification code to elect super committees and rotate them.
Wealthy validators will split their ETH across multiple validator slots to reduce yield volatility, so we lose some benefit by raising the effective balance cap.
If there is a temporary high fee or high MEV, the super committee may deliberately delay the finality to avoid being swapped out, so that the fee and MEV can continue to be charged.
Idea 2: Set the upper limit of the verifier set size
We can try one (or both) of two types of capping schemes:
Set the upper limit of the total amount of ETH pledged
Set the upper limit of the total number of verifiers
Each capping scheme can be implemented with a choice of order-based mechanisms (stacks or queues) or mechanisms regulated by economic models.
Sequence-based mechanisms have many problems. To understand why, consider two types of order-based strategies:
Keep Oldest Validator (OVS): If the set of validators is full, no one else can join
Keep Newest Validator (NVS): If the set of validators is full, then the oldest validator will be kicked out
Both categories have serious problems. OVS runs the risk of turning into a "dynasty" of early stakers who, if they leave, may lose the opportunity to rejoin forever. This also leads to MEV auctions or long queues every time a validator leaves to join the validator set. On the other hand, NVS may trigger persistent MEV auctions, which disrupt the entire chain, as validators who are kicked out will want to rejoin immediately, thus competing with genuine new players.
Set the upper limit of the total amount of ETH pledged through the economic model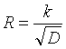
Another optional mechanism is to use an economic model to set an upper limit: if there are too many validators who want to participate, then punish all new and old validators until some validators give up and leave. A simple approach is to change the validator reward formula from the current
Change to something like: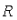
in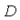
is the reward for well-behaved validators (less-performing validators receive relatively low rewards), and
is the total ETH balance of currently active validators. The curve looks roughly like this: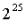
On the left side of the curve, validator rewards work in line with the current mechanism. However, as the total amount of ETH staked increases into the millions, the reward function begins to decline at an accelerated rate, dropping below zero at around 25 million ETH. In special cases where priority fees and MEV yields are sufficient to cover their losses, validators may be willing to continue staking despite zero or negative base payoffs. The reward curve is at
ETH (about 33.5 million ETH) tends to negative infinity, so that no matter how high the external reward is, the size of the validator set cannot exceed this upper limit.
The advantage of this approach is that it completely avoids the design of dynamic queues: it will reach equilibrium no matter where the equilibrium point is; the validator set size will eventually reach the equilibrium point (under current conditions, no more validators want to participate ).
The main disadvantage of this approach is the constant blocking attack near the right side of the curve: an attacker can join and quickly kick out other validators. But this is a small problem compared to other schemes, because it can only happen when the MEV is abnormally high, and this attack is very expensive (requiring millions of ETH).
Another major downside is that it could lead us towards a future where most validators are "marginalized", where large stakers outcompete smaller stakers due to their greater tolerance for earnings volatility.
Set the upper limit of the total number of verifiers through the economic model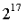
We can use the same logic to cap the validator population by adding a penalty proportional to the validator population. For example, if we want to set a validator cap of
, we can do this:
Another approach is to add a floating minimum balance: if the total number of validators exceeds the cap, the validator with the lowest balance will be kicked out.Floating minimum balances challenge a new type of malicious attack: wealthy validators divide their staked funds in order to kick out small validators (thus increasing their rewards, because the total amount of pledge
decreased). We can mitigate this by increasing the fee per validator slot to the point where such an attack is not worthwhile under the Zipf distribution. However, a potential vulnerability remains if the Zipf distribution is no longer obeyed.
An important problem with all of these proposals is that they alter existing security guarantees. especially:
Supercommittee reduces the cost of the attack chain from 1/3 of the total amount staked to about 1 to 2 million ETH.
Set the total amount of pledge or the upper limit of the total amount of verifiers through the economic model to design and change the ETH issuance formula, reduce the pledger's income, and increase malicious attacks.
Careful consideration is still needed to determine which trade-off is most acceptable to the community.
Summarize
Summarize
There are three main questions to research here:
Develop a specific consensus algorithm and combine the BFT consensus algorithm with fork selection rules to a limited extent.
Determine the best aggregation strategy to aggregate as many validator signatures as possible within a slot.
Determine the economic model for validators: If the demand to become a validator exceeds the system's ability to handle validators, then you need to answer who will stay and who will stay.
Original link
