Original source: Delphi Digital

Compilation of the original text: The Way of DeFi

key points

• Original source: Delphi Digital

• Compilation of the original text: The Way of DeFi

• key points

• Ethereum is the only major protocol building a scalable unified settlement and data availability layer

• Rollups Scale Computation While Leveraging Ethereum's Security

• All Roads Lead to Centralized Block Production, Decentralized Trustless Block Validation, and Censorship-Resistant Endgame

• MEV is now front and center - a lot of design is planned to mitigate its harm and prevent its tendency towards centralization

Introduction

Danksharding combines multiple cutting-edge research avenues to provide the scalable base layer needed for Ethereum's Rollup-centric roadmap

I do hope to achieve danksharding in our lifetime

Introduction

Part I – The Road to Danksharding

1) Raw data shard design – independent shard proposer

2) Data availability sampling

3) KZG Commitment

4) KZG Promise and Fraud Proof

8) Danksharding

5) Proposer-builder separation within the protocol

6) Anti-censorship list (crList)

7) Two-dimensional KZG scheme

9) Danksharding – honest majority verification

10) Danksharding – rebuilding

11) Danksharding – Malicious majority security with private random sampling

12) Danksharding – Key Takeaways

13) Danksharding – Limitations of Blockchain Scalability

14) Raw danksharding (EIP-4844)

15) Multidimensional EIP-1559

Part II – History and State Management

1) Reduce calldata gas by total calldata limit (EIP-4488)

5) Verkle Tries

2) Limit execution of historical data in client (EIP-4444)

3) Restore historical data

4) Weakly stateless

2) MEV-Boost

6) State expires

Part III – It's all MEV

1) Current MEV supply chain

3) Committee-driven MEV smoothing

4) Single-slot determinism

5) Single Secret Leader Election

1) The merged client

Introduction

2) Merged Consensus

concluding thoughts

Introduction

I've been skeptical of The Merge's timeline since Vitalik said that people born today have a 50-75% chance of living to 3000 years and that he hopes to live forever. However, let’s take this as a joke, anyway, we still have to look forward to Ethereum’s ambitious roadmap.This is not a quick read. If you want a broad and nuanced look at Ethereum's ambitious roadmap - give me an hour of focus and I'll save you months of work.There are a lot of Ethereum research directions to follow over the long term, but everything ultimately fits into one overarching goal — to scale computation without sacrificing decentralized validation.

Hope you are familiar with Vitalik's famous "

end game

• "One article. In his article, he admits that some centralization is needed to achieve scale. This "C" word is scary in blockchain, but it's a fact. We just need to maintain this power through decentralized and trustless verification. There is no compromise here.

• Professionals will build modules for L1 and above. Ethereum is still very secure with simple decentralized verification, and Rollup inherits their security from L1. Ethereum then provides settlement and data availability, allowing Rollups to scale. All the research here ultimately hopes to optimize these two roles, while making it easier than ever to fully verify a chain.

• Here's a glossary to abbreviate some words that will appear ~43531756765713534 times:

• DA – Data Availability

• DS–Danksharding

• DAS – Data Availability Sampling

• PBS – proposer-builder separation

PDS – raw darksharding

PoW - Proof of Work

PoS – Proof of Stake

Part I: The road to Danksharding

Hopefully you've heard by now that Ethereum has shifted to a Rollup-centric roadmap. No more sharding - Ethereum will instead be optimized for data-hungry rollups. This is achieved through data sharding (Ethereum's plan) or large blocks (Celestia's plan).

The consensus layer does not interpret sharded data. It has one job to do - make sure the data is available.

I'm assuming you're already familiar with basic concepts like Rollup, Fraud, and ZK Proofs, and why DA is important. If you're unfamiliar or just need a refresher, Can's recently published report on Celestia covers them.

Raw data shard design - independent shard proposer

The design described here is obsolete, but it is a valuable scenario. For simplicity, I'll call this "sharding 1.0".

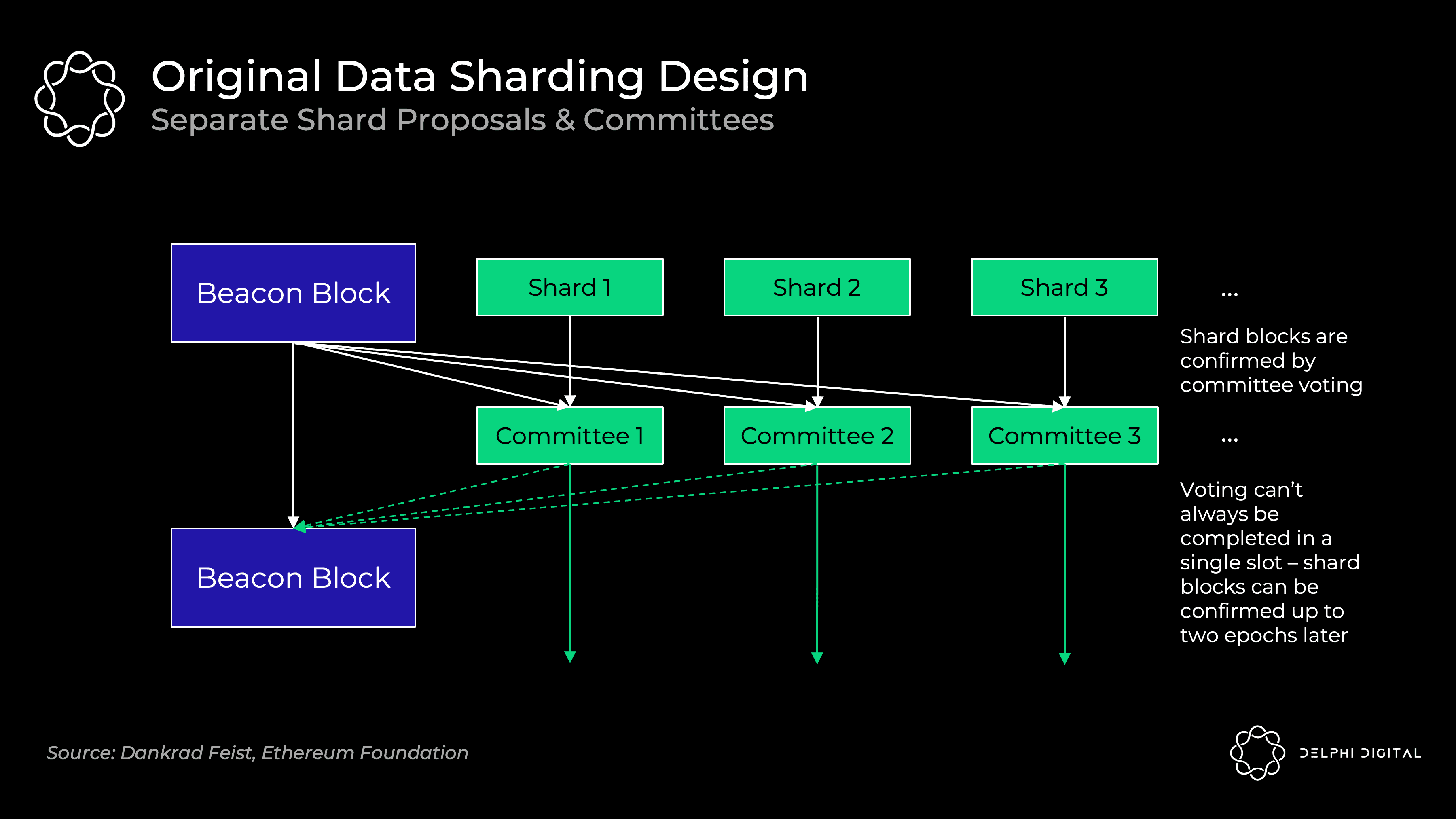
Each of the 64 shard blocks has independent proposers and committees, rotating from the set of validators. They independently verify that their shard data is available. Originally this was not DAS - it relied on a majority of each shard's validator set to fully download the data.

This design introduces unnecessary complexity, worse user experience and attack vectors. Shuffling validators between shards is tricky.

Unless you introduce very strict synchronization assumptions, it's hard to guarantee that voting will be done within a single slot. Beacon block proposers need to collect all individual committee votes, and delays may occur.

DS is completely different. Validators execute DAS to confirm that all data is available (no more separate shard committees). A specialized builder creates a large block with a beacon block and all shard data confirmed together. Therefore, PBS is necessary for DS to remain decentralized (building large blocks together is resource intensive).

• Data Availability Sampling

• Rollups publish a lot of data, but we don't want nodes to download all of this data. This would imply high resource requirements, thereby compromising decentralization.

Instead, DAS allows nodes (even light clients) to easily and securely verify that everything is available without downloading everything.

Simple solution - just check a bunch of random chunks in that block. If they all sign, I sign. But what if you miss a transaction that gives all your ETH to Sifu? Funds are no longer safe.

Smart solution - wipe the data first. Extend the data using Reed-Solomon codes. This means the data is interpolated as a polynomial, which we then evaluate in many other places. This is done in one go, so let's break it down.

For those who have difficulty understanding math, let's quickly explain. (I promise it won't be a really horrible math - I had to watch some Khan Academy videos to write the parts, but I get it now).

A polynomial is an expression that sums any finite number of terms of the form cxk. Degrees are the highest exponents. For example, 2 x3+6 x2+2 x-4 is a cubic polynomial. You can reconstruct any polynomial of degree d from any d+1 coordinate lying on that polynomial.

Now give a concrete example. Below we have four chunks of data (d0 to d3). These chunks of data can be mapped to an evaluation of the polynomial f(X) at a given point. For example, f(0) = d0. Now you have found the minimum degree polynomial that runs through these evaluations. Since this is four chunks, we can find a cubic polynomial. We can then extend this data to add four evaluations (e0 to e3) along the same polynomial.

Remember the key polynomial property - we can reconstruct it from any four points, not just our original four chunks of data.

Back to our DAS. Now we just need to make sure that any 50% (4/8) of erasure coded data is available. From this, we can reconstruct the entire block.

Therefore, an attacker would have to hide more than 50% of the blocks to successfully trick a DAS node into thinking the data is available when it is not.

After many successful random samples, the <50% available probability is very small. If we successfully sample erasure coded data 30 times, then the probability that <50% is available is 2-30.

KZG Commitment

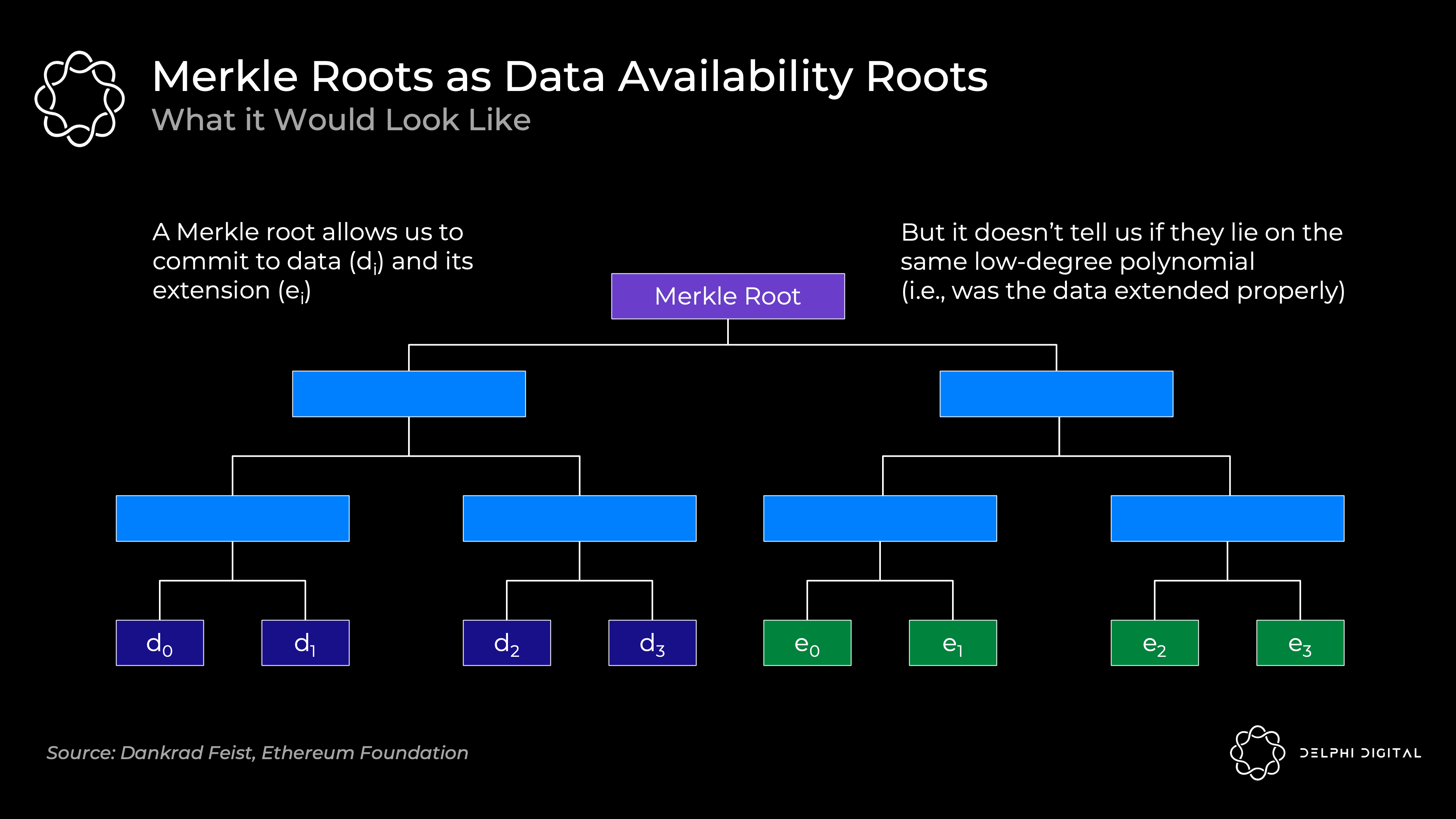
OK, so we made a bunch of random samples, and they're all available. But we have another question - is data erasure coding correct? Otherwise, maybe the block producers just added 50% garbage when extending the block, and we sampled the crap. In this case, we won't actually be able to reconstruct the data.

• Usually we just commit large amounts of data by using the Merkle root. This is effective for proving that a collection contains certain data.

• However, we also need to know that all original and extended data lie on the same low-degree polynomial. Merkle roots do not justify this. So if you use this scheme, you also need fraud proofs, just in case something is done wrong.

Developers are working in two directions:

Celestia is going the fraud prevention route. Someone needs to be aware that if a block is incorrectly erasure coded, they will submit a fraud proof to alert everyone. This requires the standard honest few assumptions and synchronicity assumptions (i.e., in addition to someone sending me a fraud proof, I also need to assume that I'm connected and will receive it within a finite amount of time).

Ethereum and Polygon Avail are taking a new route - KZG Commitments (aka Kate Commitments). This removes the honest-minority and synchronous security assumptions about fraud proofs (although they are still there to rebuild, as we'll get to shortly).

Other solutions exist but are not actively pursued. For example, you can use ZK proofs. Unfortunately, they are computationally impractical (for now). However, they are expected to improve over the next few years, so Ethereum may switch to STARK in the future, as KZG promises not to be quantum resistant.

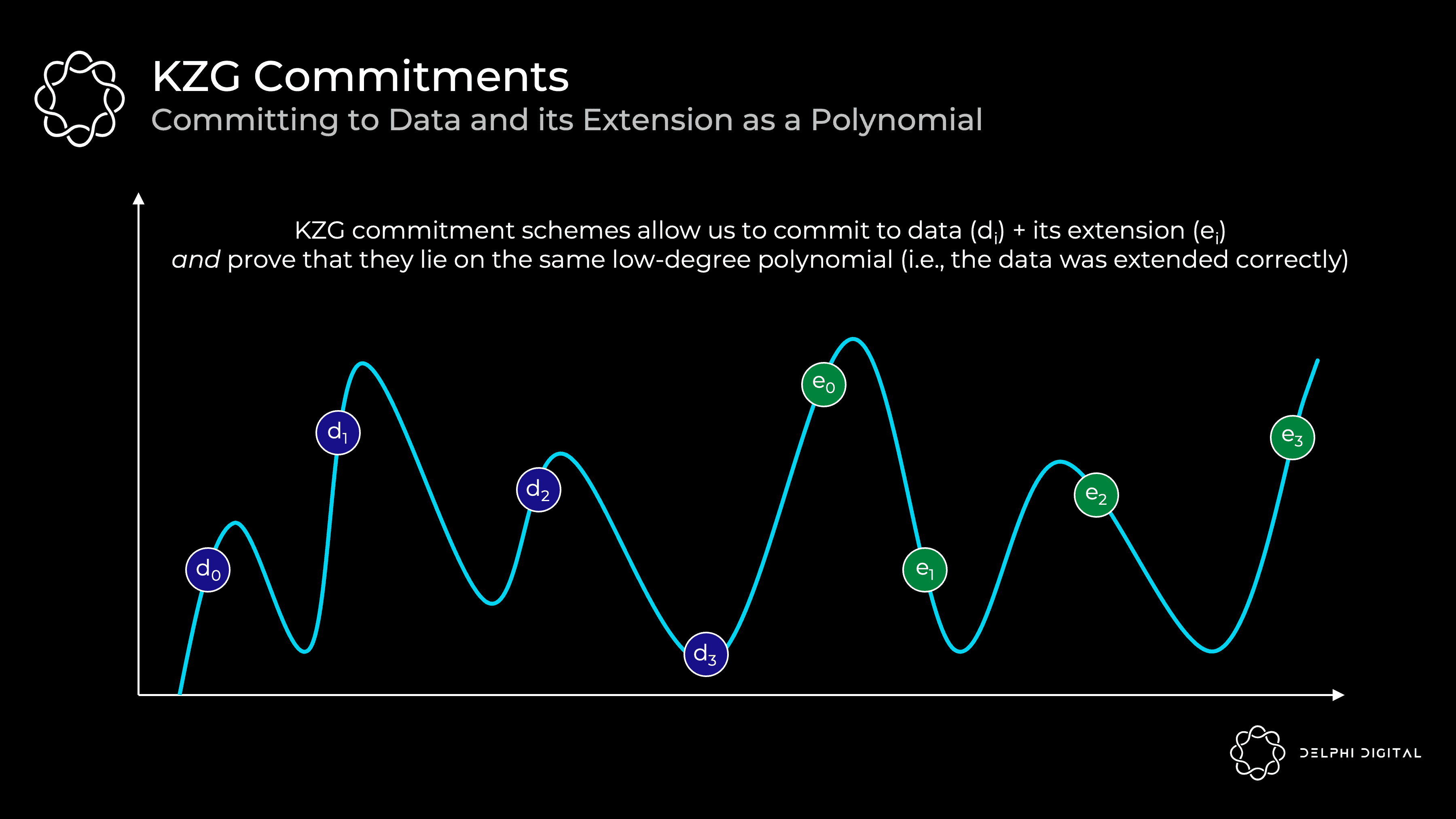
Back to the KZG commitment - this is a polynomial commitment scheme.

• A commitment scheme is simply a cryptographic way of provably committing to some value. The best analogy is putting a letter in a locked box and giving it to someone else. The letter cannot be changed once inside, but it can be opened with a key and attested. What you commit is the promise, and the key is the proof.

• In our case, we map all the original and extended data onto an X,Y grid, and then find the minimum degree polynomial that passes through them (this process is called Lagrangian interpolation). This polynomial is what the prover will promise:

Here are the key points:

• We have a "polynomial" f(X)

• The prover makes a "commitment" to the polynomial C(f)

• This relies on elliptic curve cryptography with a trusted setup. For more details on how this works, see a great post by Bartek

• For any "evaluation" of this polynomial y = f(z), the prover can compute the "proof" π(f,z)

• Given a commitment C(f), a proof π(f,z), any position z, and an evaluation y of the polynomial at z, a verifier can confirm that f(z) = y

• Explanation: The prover provides these pieces to any verifier, who can then confirm that the evaluation at some point (where the evaluation represents the underlying data) lies correctly on the committed polynomial

• This proves that the original data is scaled correctly, since all evaluations lie on the same polynomial

• Note that the verifier does not need the polynomial f(X)

• Important properties - This has O(1) commitment size, O(1) proof size and O(1) verification time. Commitment and proof generation scale only in O(d) even for the prover, where d is the degree of the polynomial

• Explanation: Even if n (number of values ​​in X) increases (i.e., as dataset increases with larger shard blobs) - promises and proofs remain the same size, and verification requires ongoing effort

Both commit to C(f) and prove that π(f,z) is just an elliptic curve element on the pair-friendly curve (this would use BL12-381). In this case, they are only 48 bytes each (very small)

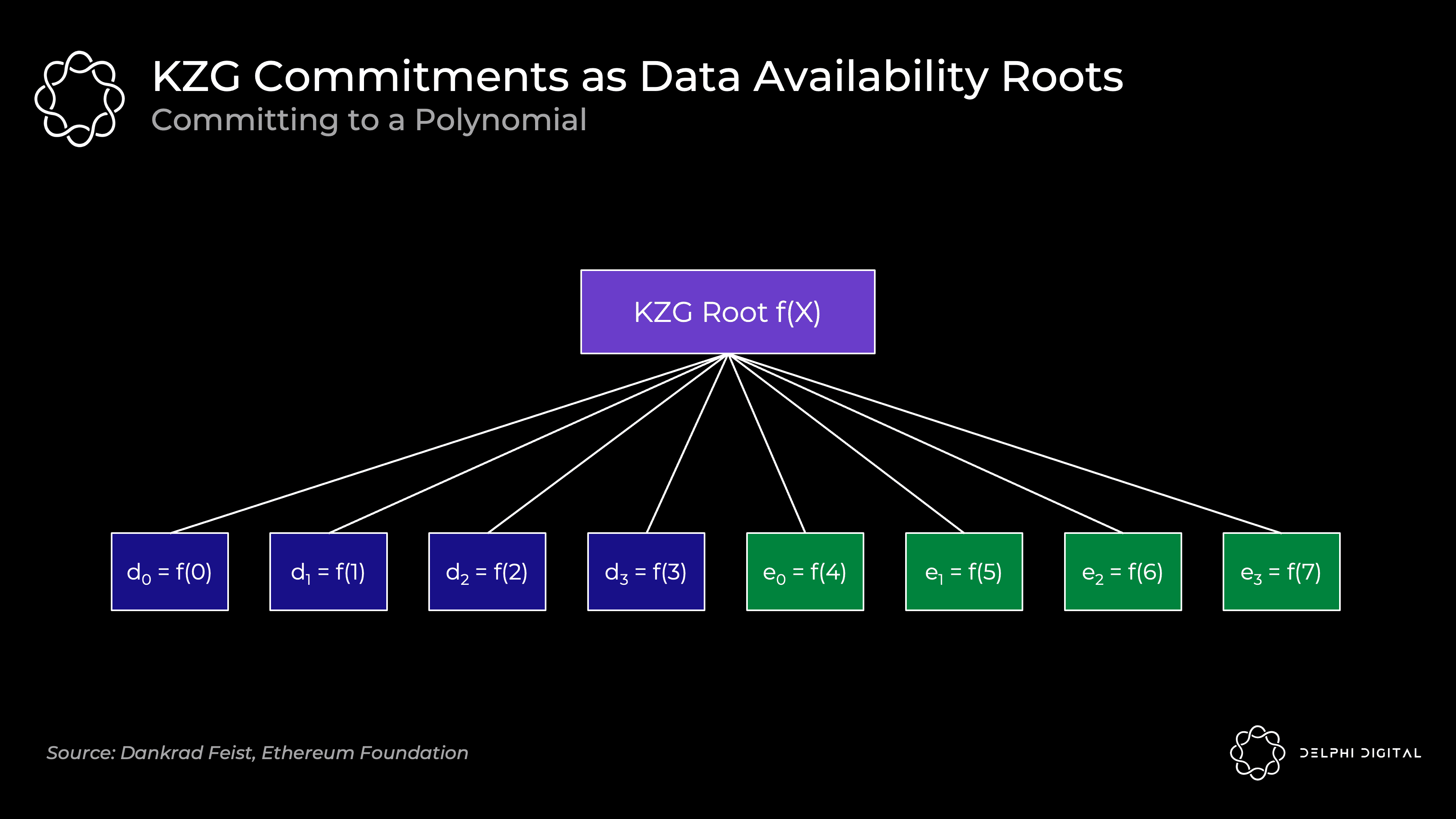
Therefore, the prover submitting a large amount of original data and extension data (representing multiple evaluations of polynomials) is still only 48 bytes, and the proof is also only 48 bytes

TLDR – this is highly scalable

Then, the KZG root (polynomial commitment) is similar to the Merkle root (which is a vector commitment):

The original data is a polynomial f (X) computed at locations f (0) to f (3), which we then expand by computing the polynomial at f (4) to f (7). All points f (0) to f (7) are guaranteed to lie on the same polynomial.

Bottom line: DAS allows us to check whether erasure coded data is available. KZG's commitment proves to us that the original data is scaled properly and promises all of them.

Well done, that's what algebra is for today.

KZG Promise and Fraud Proof

Now that we understand how KZG works, let's take a step back and compare the two approaches.

• Disadvantages of KZG - it is not post-quantum secure, it requires a trusted setup. These are not worrisome. STARK provides a post-quantum alternative, while a trusted setup (open participation) requires only one honest participant.

• Advantages of KZG - lower latency than fraud proof setups (although, as stated earlier, GASPER will not be fast finalistic anyway), and it ensures correct erasure coding without introducing the inherent Few assumptions of synchronicity and honesty.

However, given that Ethereum still reintroduces these assumptions for block reconstruction, you don't actually remove them. The DA layer always needs to plan for the scenario in which the block was initially provided, but then the nodes need to communicate with each other to put it back together. This reconstruction requires two assumptions:

You have enough nodes (light or full) sampling the data so they are good enough to put them back together. This is a fairly weak and unavoidable honest minority assumption, so not a huge problem.

Reintroducing the synchronicity assumption - nodes need to be able to communicate for a period of time in order to get it back together.

Ethereum validators fully download shard blobs in PDS, and with DS, they will only do DAS (download allocated rows and columns). Celestia will require validators to download the entire block.

• Note that in either case we need the synchronicity assumption for reconstruction. If the block is only partially available, full nodes must communicate with other nodes to put it back together.

• If Celestia were to move from requiring validators to download full data to only implementing DAS (although such a shift is not currently planned), then the latency advantage of KZG would become apparent. Then, they also need to implement KZG commitments - waiting for fraud proofs would mean significantly increasing block intervals, and the risk of validators voting for wrongly coded blocks would be very high.–Vitalik

• I recommend the following for a more in-depth exploration of how KZG promises work:–Dankrad

• A (relatively easy to understand) primer on elliptic curve cryptography–Vitalik

Exploring Elliptic Curve Pairings

KZG Polynomial Commitment

How does the trusted setting work?

Intra-protocol proposer-builder separation

Today's consensus nodes (miners) and merged ones (validators) play two roles. They build the actual block and then propose it to other consensus nodes who validate it. Miners "vote" on the basis of the previous block, and after merging, verifiers will directly vote on whether the block is valid or invalid.

PBS separates them - it explicitly creates a new in-protocol builder role. Professional builders will put blocks together and bid on proposers (validators) to choose their blocks. This fights against the centralized power of MEV.

1. Recall Vitalik's "Endgame" article - all roads lead to centralized block production with trustless and decentralized validation. PBS compiled this. We need an honest builder to serve the network for liveness and censorship resistance (two are needed for an efficient market), but an honest majority is needed for the validator set. PBS makes the proposer role as simple as possible to support validator decentralization.

2. Builders receive a priority fee tip along with any MEV they can withdraw. In an efficient market, competitive builders will bid for the full value they can extract from a block (minus their amortized costs such as powerful hardware, etc.). All value permeates the decentralized validator set - exactly what we want.

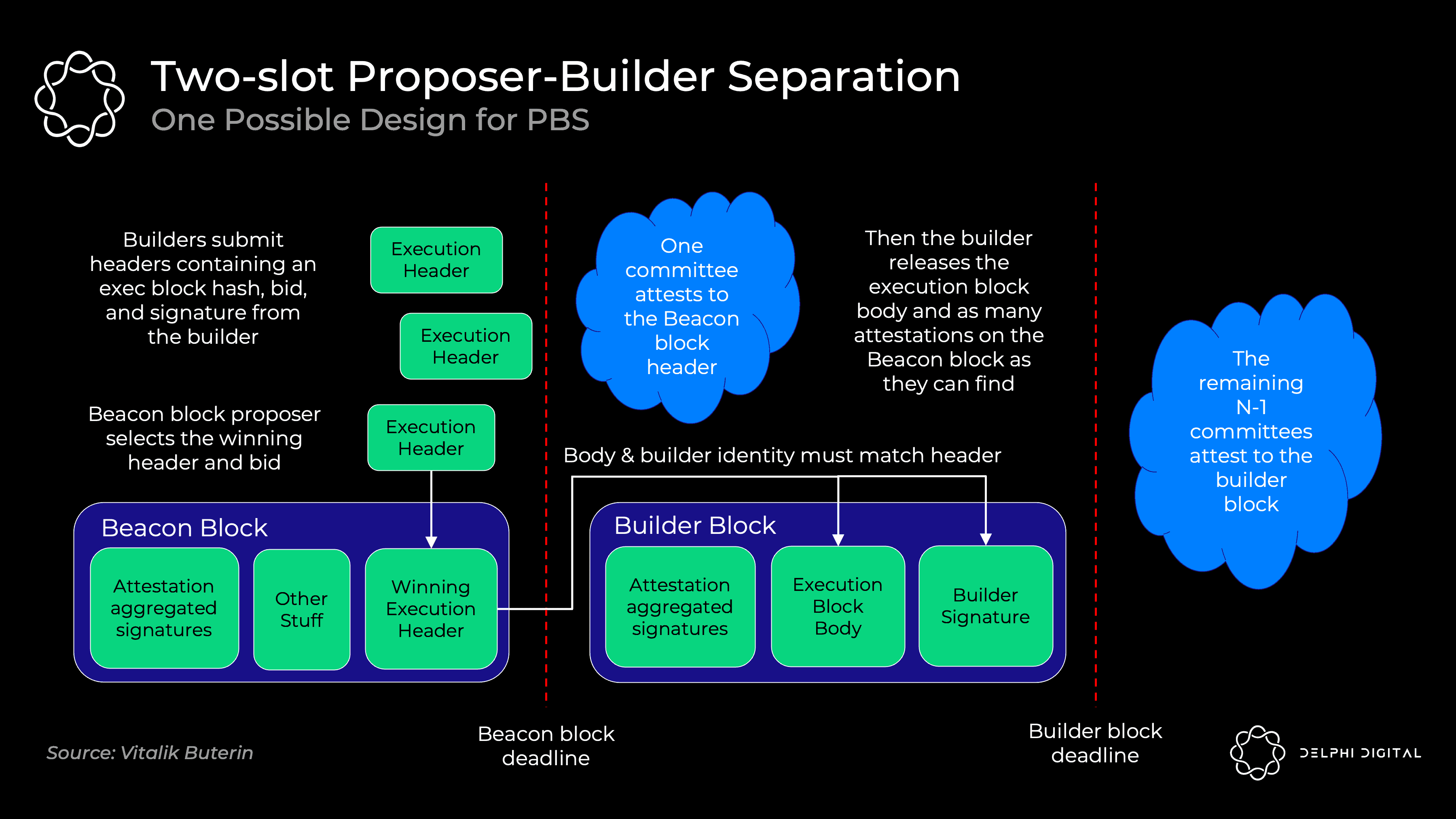
3. The exact PBS implementation is still under discussion, but a two-slot PBS might look like this:

4. Builders commit block headers with their bid

5. The beacon block proposer selects the winning block header and bid. Even if the builder fails to produce the body, the bidder will win the bid unconditionally

Proof committee confirms winning header

The builder announces the winning body

Independent committee of witnesses elects the winning body (if the winning builder disagrees, it is voted absent)

Proposers are selected from the set of validators using the standard RANDAO mechanism. We then use a commit-reveal scheme where the full block body is not revealed until the committee confirms the block header.

commit-reveal is more efficient (sending around hundreds of full block bodies can overwhelm p2 p-layer bandwidth), and it also prevents MEV stealing. If a builder were to submit their full block, another builder could see it, figure out that strategy, merge it, and quickly publish a better block. Furthermore, mature proposers can detect the MEV strategy used and replicate it without compensating builders. If this MEV stealing becomes balanced, it will incentivize merge builders and proposers, so we use commit-reveal to avoid this.

After the proposer elects the winning block header, the committee confirms and fixes in the fork selection rules. The winning builders then publish their winning full "builders block" body. If released in time, the next committee will testify. If they fail to publish in time, they still pay the proposer the full bid (and lose all MEV and fees). This unconditional payment removes the need for proposers to trust builders.

The downside of this "two-slot" design is latency. The merged block will be a fixed 12 seconds, so here we need 24 seconds to get the full block time (two 12 second slots) if we don't want to introduce any new assumptions. 8 seconds per slot (16 second block time) seems like a safe compromise, although research is ongoing.

1. Censorship Resistance List (crList)

2. Unfortunately, PBS gives builders a higher ability to review transactions. Maybe the builders just don't like you, so they ignore your deal. Maybe they're doing such a good job that all the other builders give up, or maybe they're just overbidding on blocks because they really don't like you.

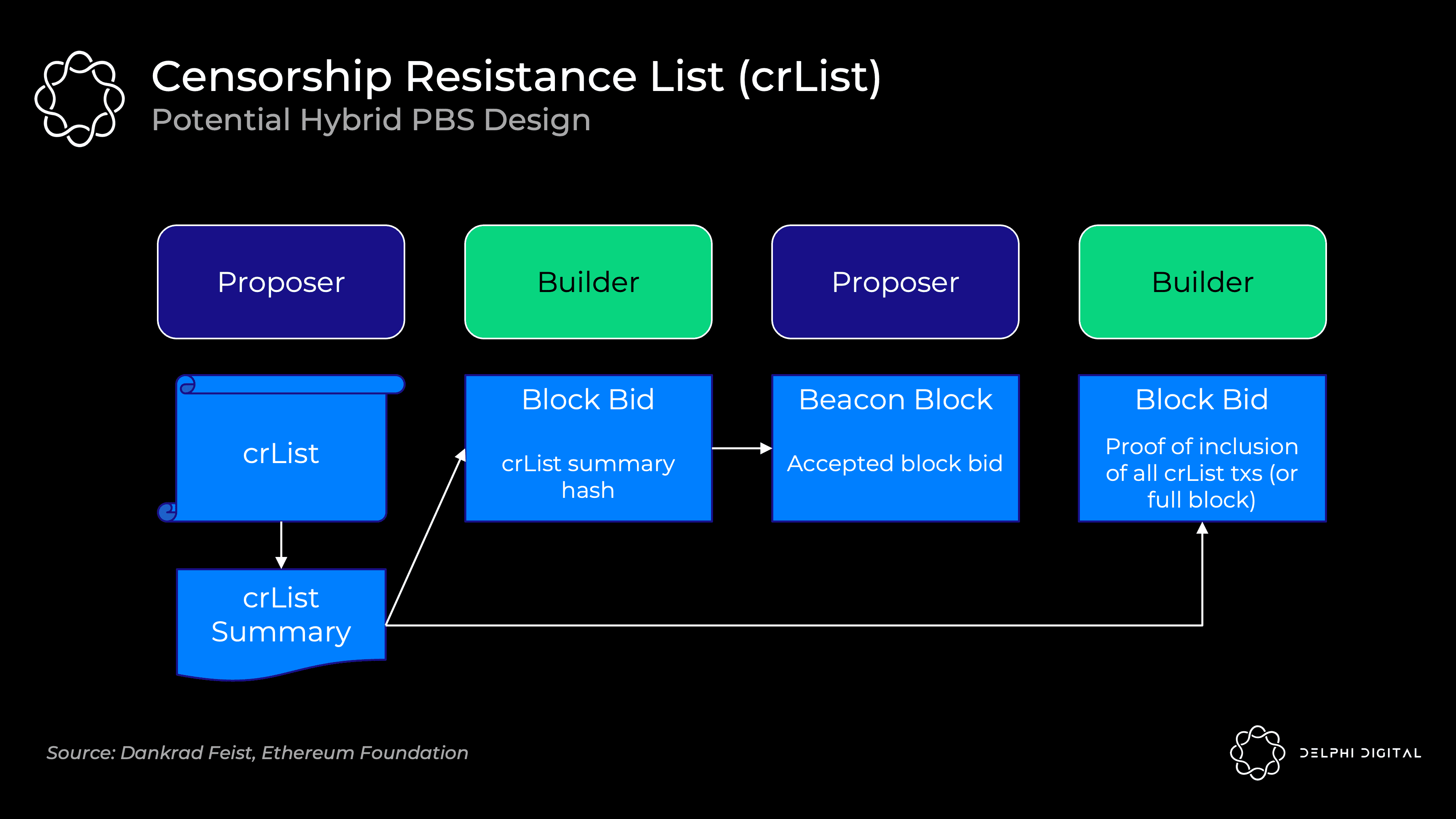
3. crLists checks for this capability. The exact implementation is again an open design space, but "hybrid PBS" seems to be the favorite. Proposers specify a list of all eligible transactions they see in the mempool, and builders will be forced to include them (unless the block is full):

4. The proposer publishes a crList and a digest of the crList which includes all eligible transactions

5. Builders create a proposed block body, then submit a bid that includes a hash of the crList digest proving they have seen it

The proposer accepts the winning builder's bid and block header (they haven't seen the body yet)

Builders publish their blocks and include proof that they have included all transactions from crList or that the block is full. Otherwise the fork choice rule will not accept the block

The prover checks the validity of the published body

There are still important issues to be resolved here. For example, the dominant economic strategy here is to have proposers submit an empty list. Even a review builder can win the auction as long as the highest bid is made. There are some ideas to solve this and other problems, but just to emphasize that the design here is not set in stone.

Two-dimensional KZG scheme

We saw how KZG promises allow us to commit to data and prove that it was scaled correctly. However, I simplified the actual operation of Ethereum. It will not commit all data in a single KZG commitment - a single block will use many KZG commitments.

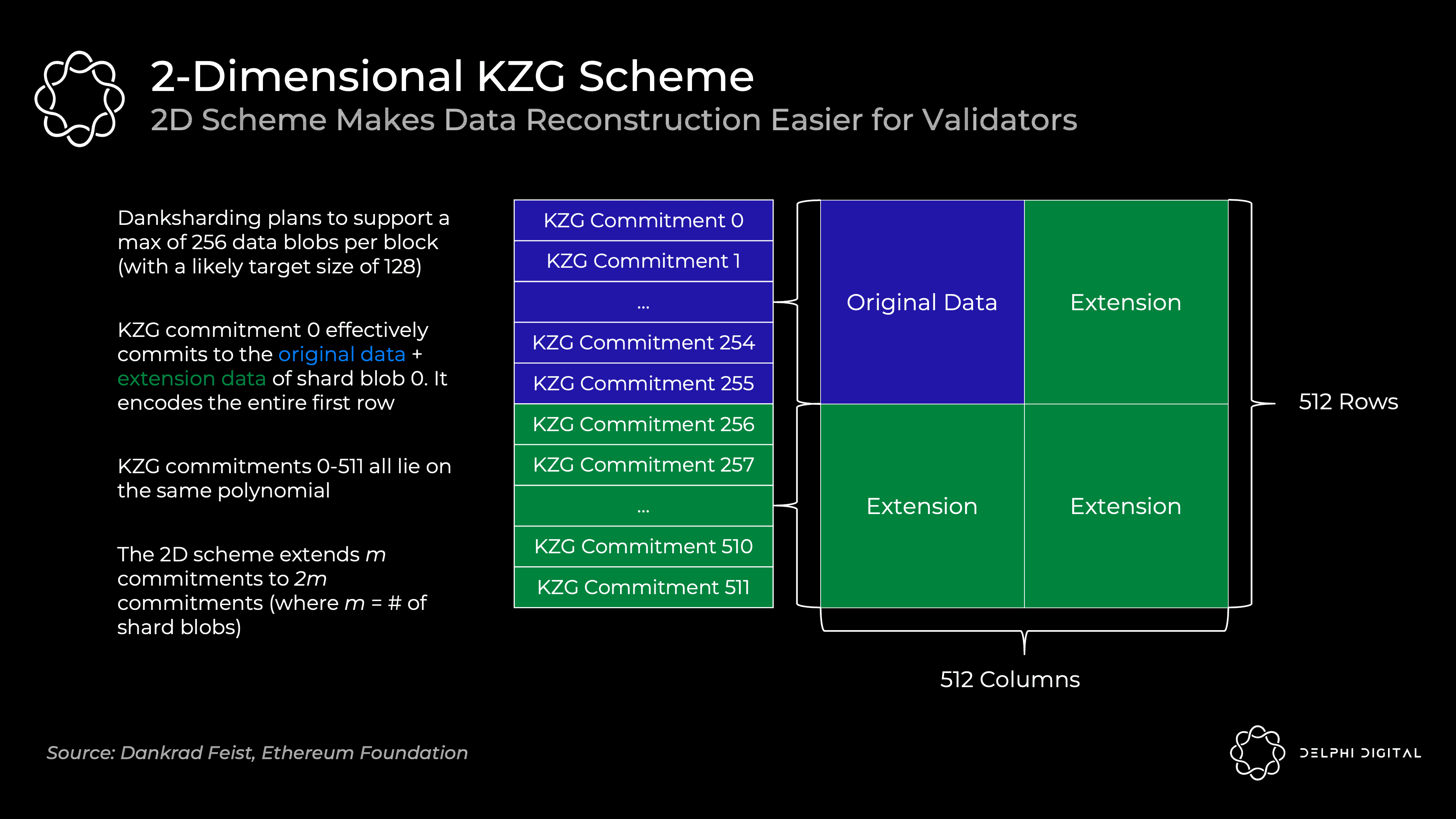
We already have a dedicated builder, so why not let them create a giant KZG commit? The problem is that this requires a powerful supernode to rebuild. We can live with the supernode requirements for the initial build, but we need to avoid rebuilding assumptions here. We need less resourceful entities to handle the rebuild, and splitting it into many KZG commits makes this feasible. Given the amount of data at hand, reconstruction might even be fairly common, or the base case assumption in this design.

To make reconstruction easier, each block will contain m shard blobs encoded in m KZG commitments. Doing this naively will result in a lot of sampling - you'll do DAS on each shard blob until it's all available (m*k samples, where k is the number of samples per blob).

Instead, Ethereum will use a 2D KZG scheme. We again use the Reed-Solomon code to scale m commitments to 2 m commitments:

We make it a 2D scheme by extending the additional KZG commitment on the same polynomial as 0-255 (here 256-511). Now we just need to DAS the above table to ensure data availability for all shards.

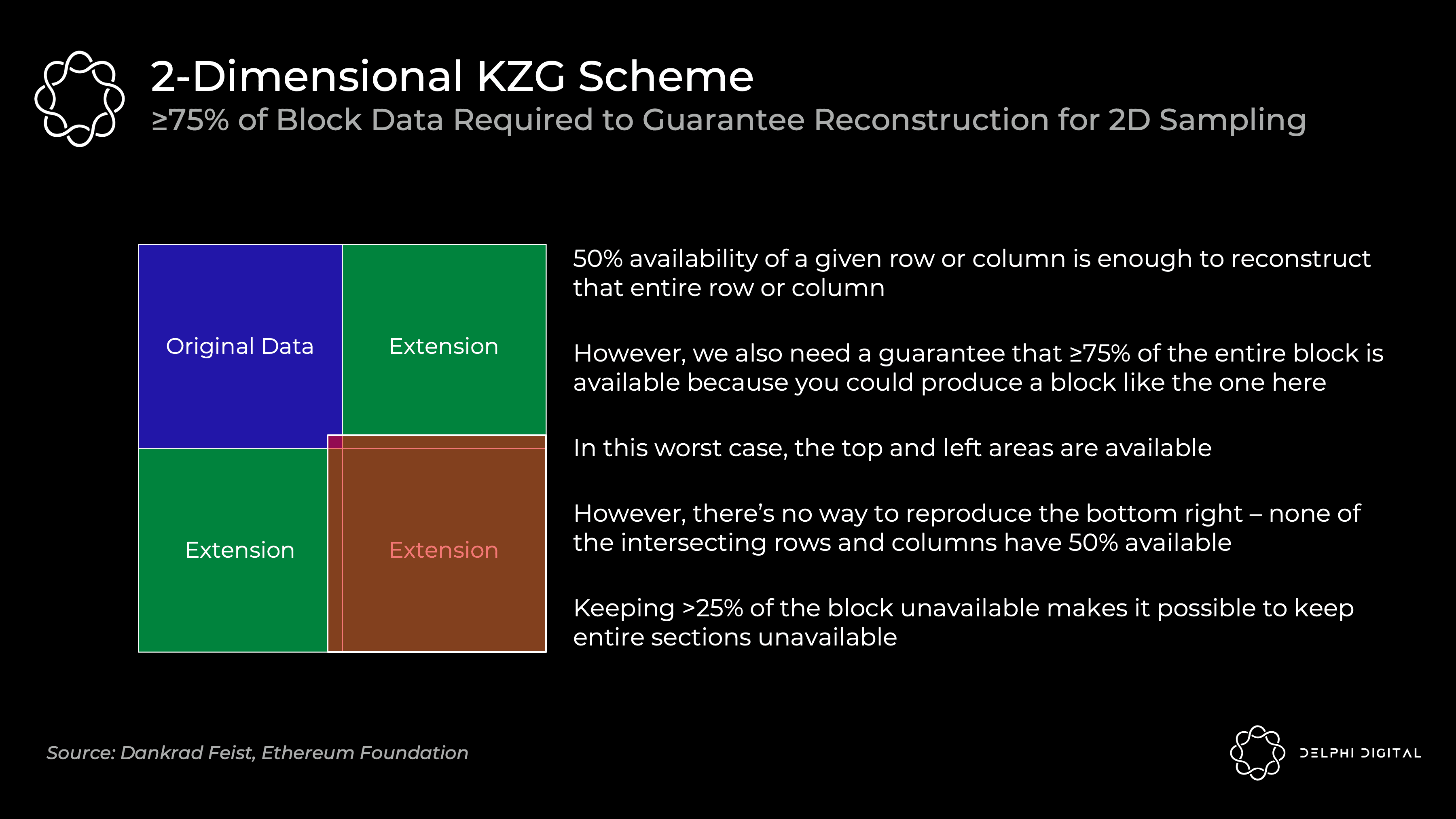
The 2D sampling requirement of ≥75% of the data available (compared to 50% previously) means we do a bit more fixed sample size. Before I mentioned 30 samples for DAS in the simple 1D scheme, but this would require 75 samples to ensure the same probabilistic odds of reconstructing usable blocks.

Sharding 1.0 (with a 1D KZG commitment scheme) requires only 30 samples, but if you want to check the full DA of 1920 samples, you need to sample 64 shards. Each sample is 512 B, so this requires:

(512 B x 64 slices x 30 samples) / 16 seconds = 60 KB/s bandwidth

Danksharding

Effectively, validators are simply shuffled without checking all shards individually.

Compositional blocks using a 2D KZG commitment scheme now make checking the full DA trivial. It only requires 75 samples of a single uniform block:

(512 B x 1 block x 75 samples) / 16 seconds = 2.5 KB/s bandwidth

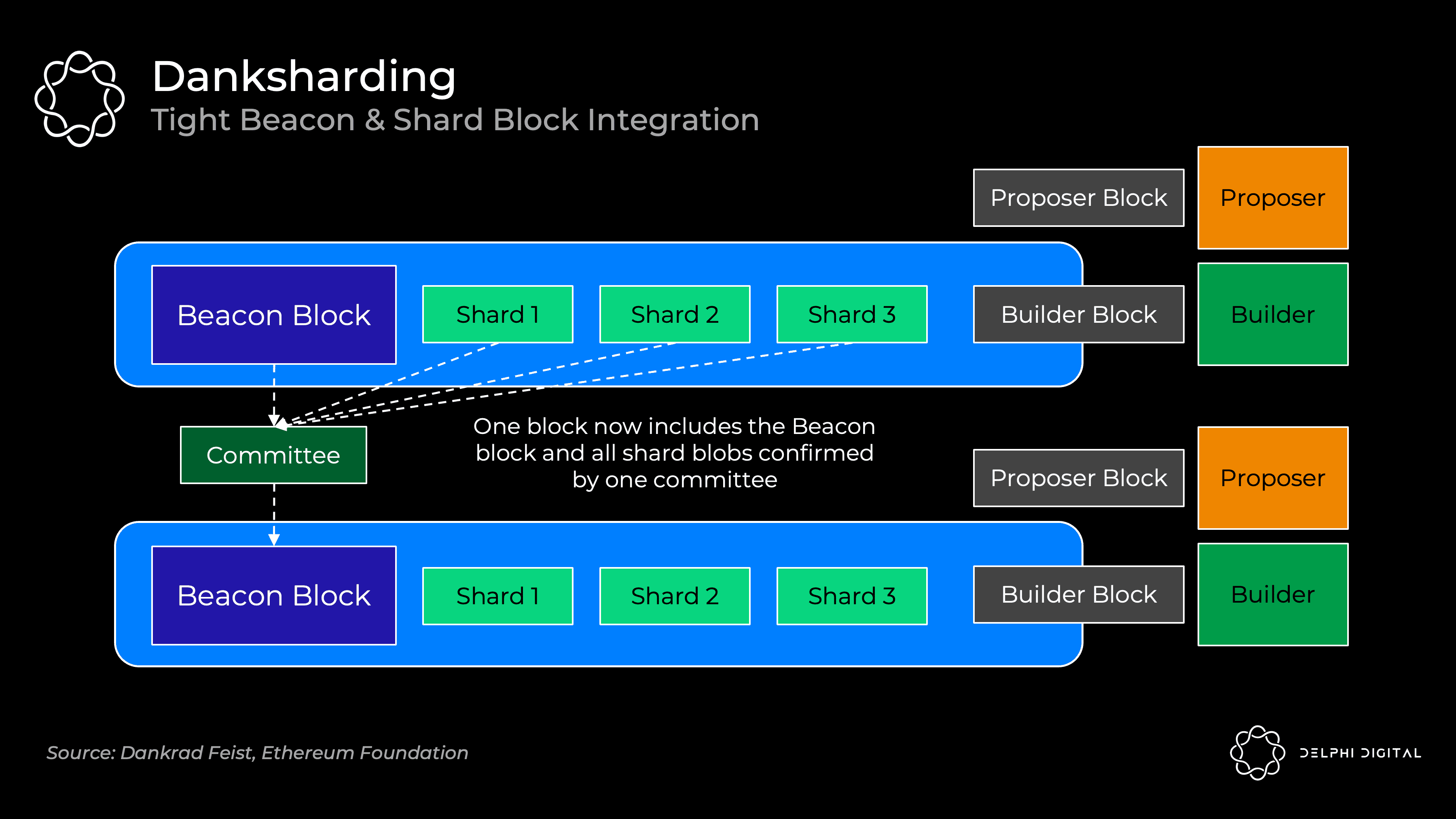
PBS was originally designed to reduce MEV's concentration on the validator set. However, Dankrad recently took advantage of this design, realizing that it unlocked a much better sharding structure - DS.

DS leverages dedicated builders to create a beacon chain that enforces tighter integration of blocks and shards. We now have a builder that together creates the entire block, a proposer and a committee. DS would be infeasible without PBS - regular validators cannot handle the huge bandwidth of blocks full of Rollup data blobs:

Sharding 1.0 includes 64 independent committees and proposers, so each shard may be individually unavailable. The tighter integration here allows us to ensure DA all at once. Data is still "sharded" behind the scenes, but from a practical standpoint, danksharding is starting to feel more like big blocks, which is great.

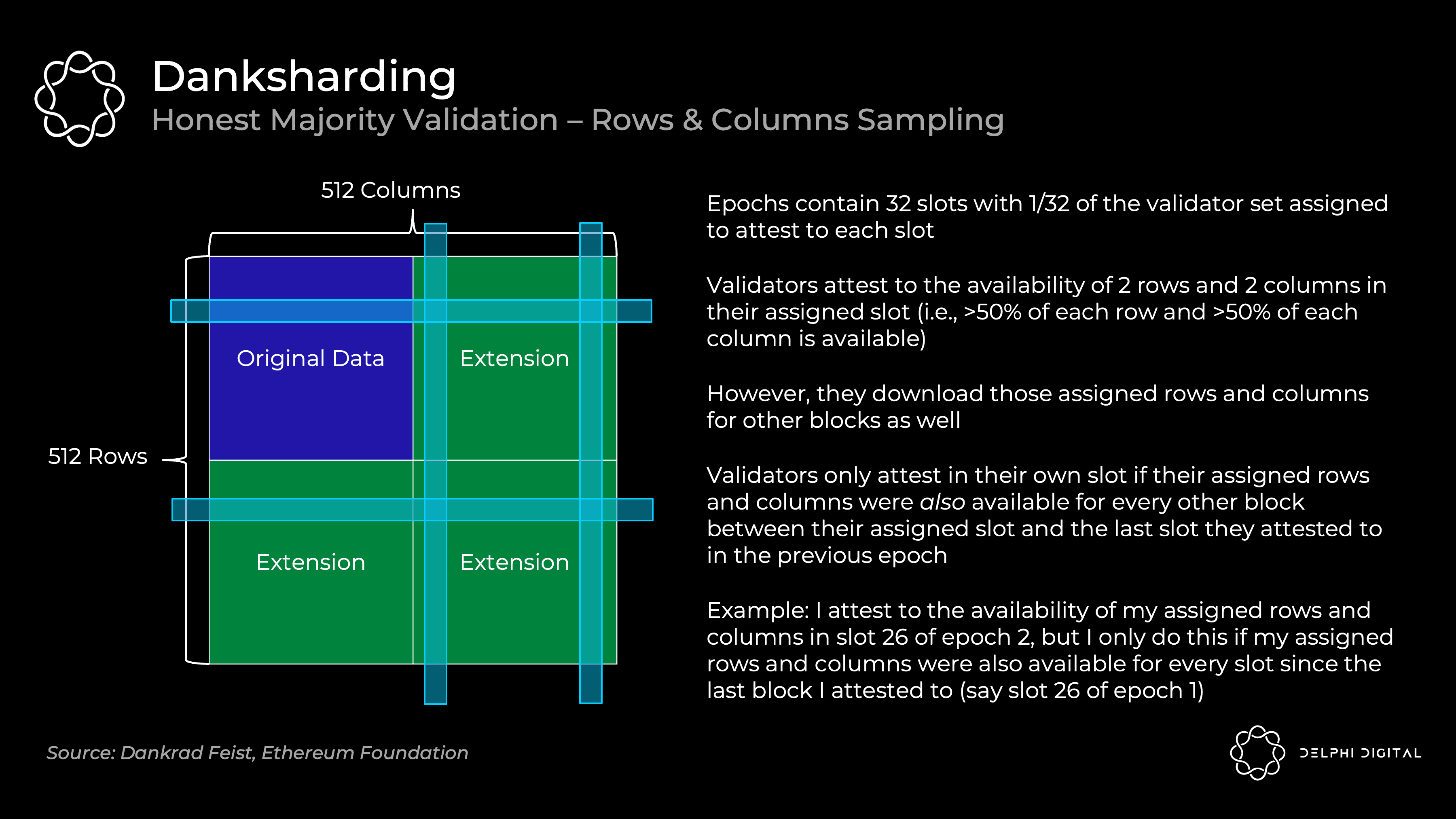
Danksharding – honest majority verification

Verifier proof data is available as follows:

This relies on an honest majority of validators - as a single validator, my column and row availability is not enough for me to be statistically confident that the entire block is available. It depends which honestly most people say it is. Decentralized validation is important.

Note that this is different from the 75 random samples we discussed earlier. Private random sampling is how resource-poor individuals can easily check availability (for example, I can run a DAS light node and know the block is available). However, validators will continue to use the row and column approach to check availability and guide block reconstruction.

• Danksharding - refactoring

• As long as 50% of a single row or column is available, the sampling validator can easily reconstruct it completely. When they reconstruct any blocks that were lost in a row/column, they reassign those blocks to orthogonal lines. This helps other validators reconstruct any missing blocks from intersecting rows and columns as needed.

The safe assumptions for rebuilding usable blocks here are:

Enough nodes to perform sample requests so that they collectively have enough data to reconstruct the block

Synchronization assumption between nodes broadcasting their respective blocks

So, how many nodes are enough? A rough estimate is about 64,000 individual instances (over 380,000 so far). This is also a very pessimistic calculation that assumes no crossover among nodes run by the same validator (which is a far cry from nodes being limited to 32 ETH instances). If you sample more than 2 rows and columns, the chances that you can retrieve them collectively increase due to crossover. This starts to scale quadratically - 64,000 could be orders of magnitude less if validators are running 10 or 100 validators.

If the number of online validators starts to become abnormally low, DS can be set up to automatically reduce the shard data blob count. Therefore, the safety assumption will be reduced to a safe level.

Danksharding – Malicious majority security with private random sampling

We saw that DS validation relies on an honest majority to attest to blocks. As an individual, I cannot prove to myself that a block is available by downloading only a few rows and columns. However, private random sampling can give me that assurance without trusting anyone. As mentioned earlier, this is where the node checks the 75 random samples.

DS will not initially include private random sampling, as this is a very hard problem to solve in terms of networking (PSA: maybe they could actually use your help here!).

Note that "private" is important because if an attacker deanonymizes you, they will be able to spoof a small number of sampled nodes. They can just return the exact block you requested and keep the rest. Therefore, you don't know that all the data is available just from your own sampling.

Danksharding – key takeaways

Besides being a sweet name, DS is also very exciting. It finally realizes the vision of Ethereum's unified settlement and DA layer. This tight coupling of beacon blocks and sharding essentially pretends not to be sharded.

• In fact, let's define why it's even considered "sharding". The only remnant of "sharding" is that validators are not responsible for downloading all the data. That's all.

• So if you're now questioning whether this is really still sharding, you're not crazy. This distinction is why a PDS (which we'll get to shortly) isn't considered a "shard" (even though it has "shard" in its name, yes, I know that's confusing). PDS requires each validator to fully download all shard blobs to prove their availability. DS then introduces sampling, so each validator only downloads a portion of it.

• Fortunately, minimal sharding means a simpler design than sharding 1.0 (delivering so fast, right?). In short, it includes:

Compared to the sharding 1.0 spec, there are probably hundreds of lines less code in the DS spec (thousands less on the client side)

No shard committee infrastructure, committees only need to vote on the main chain

Individual shard blob confirmations are not tracked, they are all confirmed in the main chain now, or they are not

A nice consequence of this is a consolidated fee market for data. Sharding 1.0 with different blocks made by different proposers would spread this out.dAMMThe removal of shard committees also strengthens anti-bribery. DS validators vote on the entire block once per epoch, so the data is immediately confirmed by 1/32 of the entire validator set (32 slots per epoch). Shard 1.0 validators also vote once per epoch, but each shard has its own committee reshuffled. Therefore, each shard is only confirmed by 1/2048 of the validator set (1/32 divided into 64 shards).

Combining blocks with the 2D KZG commitment scheme also makes DAS more efficient, as mentioned earlier. Sharding 1.0 requires 60 KB/s of bandwidth to check the full DA of all shards. DS requires only 2.5 KB/s.

Another exciting possibility exists in DS - synchronous calls between ZK-rollups and L1 Ethereum execution. Transactions from shard blobs can be confirmed and written to L1 immediately, since everything is generated in the same beacon chain block. Sharding 1.0 will eliminate this possibility due to separate shard confirmations. This allows for an exciting design space, which is useful for shared mobility (e.g.

) and the like can be very valuable.

• The modular base layer scales gracefully — more decentralization leads to more scaling. This is fundamentally different from what we see today. Adding more nodes to the DA layer allows you to safely increase data throughput (ie, more room for rollups to exist on top).

• There are still limits to blockchain scalability, but we can improve orders of magnitude higher than anything we've seen today. Secure and scalable base layers allow execution to proliferate on top of them. Improvements in data storage and bandwidth will also allow for higher data throughput over time.

It is certainly possible to exceed the DA throughput envisaged here, but it is difficult to say where this maximum will end up. There are no clear red lines, but areas where some assumptions start to feel uncomfortable:

Proto-danksharding (EIP-4844)

Data Storage - This is about DA and data retrievability. The role of the consensus layer is not to guarantee the retrievability of data indefinitely. What it does is make it available long enough for anyone who cares to download it, satisfying our security assumptions. Then it gets dumped everywhere - which is comfortable because history is 1 in the N trust assumption, and we're not really talking that much data in the grand scheme of things. This could enter troubling territory in a few years as throughput increases by several orders of magnitude.

Verifier - DAS needs enough nodes to jointly rebuild the block. Otherwise, attackers may wait and only respond to queries they receive. If these queries provided are not enough to reconstruct the block, then the attacker can keep the rest and we are out of luck. To safely increase throughput, we need to add more DAS nodes or increase their data bandwidth requirements. This is not a throughput issue as discussed here. However, this can be uncomfortable if the throughput increases several orders of magnitude further than this design.

Note that the builder is not the bottleneck. You need to generate KZG proofs quickly for 32 MB of data, so a GPU or reasonably powerful CPU with at least 2.5 GBit/s of bandwidth is required. Regardless, it's a specialized role, and it's a negligible business cost to them.

DS is great, but we have to be patient. PDS is designed to tide us over - it implements the necessary forward compatibility steps for DS on an accelerated timeline (for the Shanghai hard fork) to provide orders of magnitude scaling in the meantime. However, it does not actually implement data sharding (i.e. validators need to download all data individually).

Rollups today use L1 "calldata" for storage, which lives on-chain forever. However, Rollup only requires DA for a reasonable period of time, so that anyone interested has enough time to download it.

EIP-4844 introduces a new transaction format that supports blobs, and Rollup will be used for future data storage. Blobs carry large amounts of data (~125 KB), and they are much cheaper than a similar amount of calldata. The data blobs are then deleted from the nodes after a month, which reduces storage requirements. This is enough time to satisfy our DA security assumption.

Current Ethereum blocks typically average around 90 KB (of which the call data is about 10 KB). PDS unlocks more DA bandwidth for blobs (target ~1 MB and max ~2 MB) as they get pruned after a month. They do not become a permanent drag on the node.

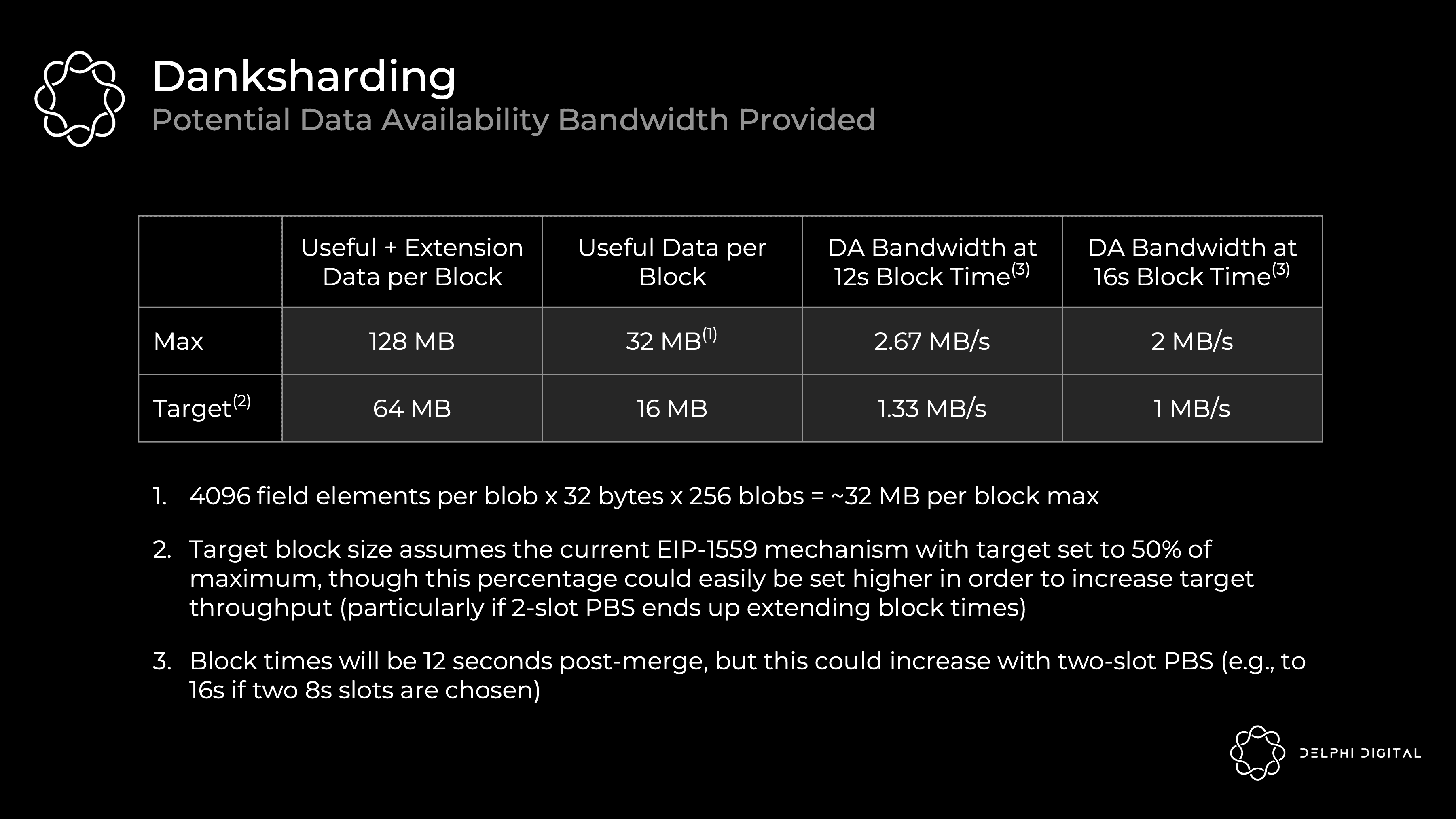
A blob is a vector of 4096 field elements, each field element is 32 bytes. PDS allows up to 16 per block, while DS will increase to 256.

PDS DA bandwidth = 4096 x 32 x 16 = 2 MiB per block with a target of 1 MiB

• DS DA Bandwidth = 4096 x 32 x 256 = 32 MiB per block with a target of 16 MiB

• Transaction format for carrying data blobs

• All execution layer logic required by DS

• All execution/consensus cross-validation logic required by DS

• KZG commitment to blobs

• All execution layer logic required by DS

• All execution/consensus cross-validation logic required by DS

Layer separation between BeaconBlock authentication and DAS blobs

• PBS

• Most of the BeaconBlock logic required by DS

• Self-adjusting independent gas prices for blobs (multidimensional EIP-1559 with exponential pricing rules)

• DS then adds further:

data collection system

2D KZG scheme

Proof of Escrow or similar in-protocol requirement for each validator to verify the availability of a specific portion of the shard's data in each block (perhaps on the order of a month)

Note that these data blobs are introduced as a new transaction type on the execution chain, but they impose no additional requirements on the execution side. The EVM only looks at commitments attached to blobs. Implementation layer changes made using EIP-4844 are also forward compatible with DS, and no further changes are required in this regard. Then upgrading from PDS to DS only requires changing the consensus layer.

• Data blobs are fully downloaded by consensus clients in PDS. Now, the blob is referenced in the Beacon block body, but not fully encoded. Instead of embedding the entire content in the body, the content of the blob is propagated separately, as a "sidecar". Each block has a blob sidecar that is fully downloaded in PDS and then using DS validators will execute DAS on it.

• We previously discussed how to commit blobs using KZG polynomial commitments. However, instead of using KZG directly, EIP-4844 implements what we actually use - its versioned hash. This is a 0x01 byte (representing this version) followed by the last 31 bytes of the KZG's SHA256 hash.

We do this for easier EVM compatibility and forward compatibility:

EVM Compatibility – KZG commitments are 48 bytes, while EVM more naturally uses 32 byte values

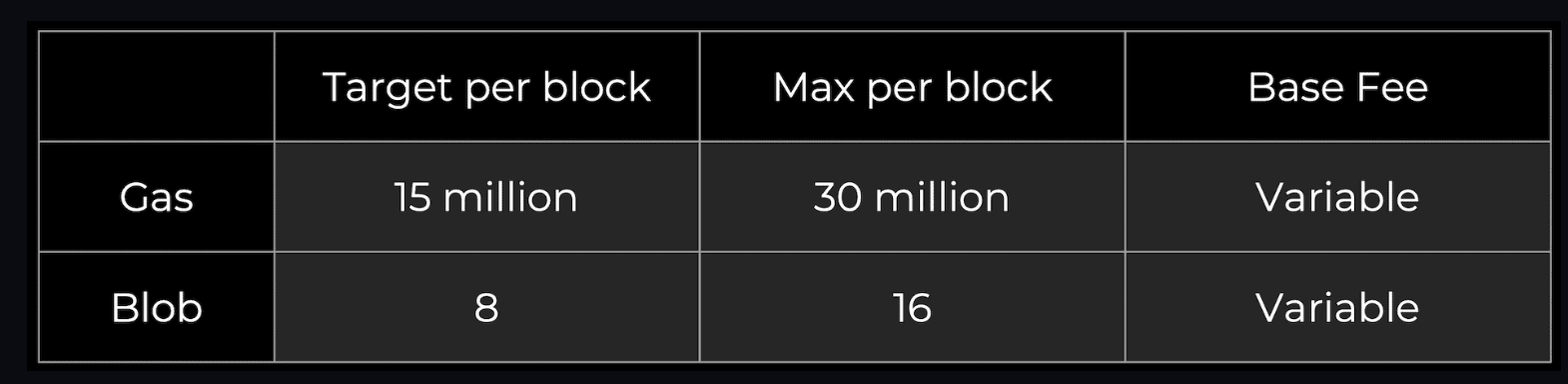
Forward compatibility - if we switch from KZG to something else (STARKs can be used for quantum resistance), these promises can continue to be 32 bytes

PDS ultimately creates a custom data layer - data blobs will have their own unique fee market with individual floating gas prices and limits. So even if some NFT project sells a bunch of monkey land on L1, your Rollup data costs won't go up (although proof settlement costs will). This acknowledges that the main cost of any Rollup today is publishing their data to L1 (not proofs).The gas fee market remains the same, data blobs are added as a new market:The blob fee is charged in gas, but it is a variable amount adjustment based on its own EIP-1559 mechanism. The long-term average number of blobs per block should be equal to the target.

You actually have two auctions running in parallel - one for computation and one for DA. this is valid

resource pricing

giant leap.

• Here are some interesting designs. For example, it might make sense to change the current gas and blob pricing mechanism from linear EIP-1559 to a new exponential EIP-1559 mechanism. The current implementation does not average out to our target block size in practice. Today, the base fee has not fully stabilized, causing the observed average gas used per block to exceed the target by an average of ~3%.

• Part II: History & State Management

A quick recap of some basics here:

History — everything that happened on-chain. You can stick it on your hard drive since it doesn't need fast access. In the long run, 1 of N honesty assumes.

State - a snapshot of all current account balances, smart contracts, etc. Full nodes (currently) all need this to validate transactions. It's too big for RAM, and the hard drive is too slow - it's in your SSD. High-throughput blockchains inflate their state far beyond what our average person can keep on his laptop. If everyday users can't hold state, they can't fully verify, so say goodbye to decentralization.

Calldata Gas cost reduction and total Calldata limit (EIP-4488)

EIP-4488 has two main components:

• The PDS is an important stepping stone to the DS and it checks many final requirements. Implementing PDS within a reasonable time span can advance the timeline on DS.

• An easier band-aid implementation is EIP-4488. It's not as elegant, but it still solves the fee emergency. Unfortunately, it does not implement steps in the process of implementing DS, so all the inevitable changes will still be required later. If it starts to feel like PDS is going to be a bit slower than we'd like, it might make sense to quickly pass EIP-4488 (it's just a few lines of code changes) and then implement PDS about 6 months later. A specific timetable has yet to be determined.

EIP-4488 has two main components:

Reduced calldata cost from 16 gas per byte to 3 gas per byte

Adds a limit of 1 MB call data per block and an additional 300 bytes per transaction (theoretical maximum is about 1.4 MB)

Limits need to be added to prevent the worst case - a block full of calldata will reach 18 MB, which is far beyond what Ethereum can handle. EIP-4488 increases the average data capacity of Ethereum, but due to this calldata limit (30 million gas / 16 gas per calldata byte = 1.875 MB), its burst data capacity will actually decrease slightly.

The sustained load of EIP-4488 is much higher than PDS, because this is still calldata and blob, data that can be pruned after a month. EIP-4488 will significantly accelerate historical growth, making it a bottleneck for running nodes. Even if EIP-4444 is implemented alongside EIP-4488, this will only delete execution load history after one year. A lower sustained load on the PDS is clearly desirable.

Bind historical data in execution client (EIP-4444)

EIP-4444 Allow clients to choose to locally prune historical data (headers, body, and receipts) older than one year. It requires clients to stop serving these pruned historical data on the p2p layer. Pruning history allows customers to reduce users' disk storage requirements (currently hundreds of gigabytes and growing).devp2pThis is already important, but if EIP-4488 is implemented (as it significantly grows history), it will be largely mandatory. Regardless, hopefully this will be done relatively soon. Eventually some form of historical expiration will be required, so this is a good time to deal with it.

Full synchronization of the chain requires history, but validating new blocks does not require it (this requires only state). Therefore, once a client has synced to the top of the chain, historical data will only be retrieved if explicitly requested via JSON-RPC or when a peer attempts to sync the chain. With EIP-4444 implemented, we need to find alternative solutions for these.

The client will not be able to use the current

Do a "full sync" - they will instead "checkpoint sync" from the weak subjectivity checkpoint, which they see as the genesis block.

Note that weak subjectivity would not be an additional assumption - it is inherent in the move to PoS anyway. Due to the possibility of remote attacks, this needs to be synchronized using effectively weak subjectivity checkpoints. The assumption here is that clients will not sync from invalid or old weak-subjectivity checkpoints. This checkpoint has to be within the period when we start pruning the historical data (i.e. within a year here), otherwise the p2p layer will not be able to provide the required data.

• This will also reduce bandwidth usage on the network as more and more clients adopt a lightweight sync strategy.

• Retrieve historical data

• EIP-4444 pruning historical data after a year sounds good, while PDS prunes blobs faster (after about a month). We absolutely need these because we can't ask nodes to store all of them and keep them decentralized:

EIP-4488 – long-term likely to include about 1 MB per slot adding about 2.5 TB of storage per year

DS – Target ~16 MB per slot, adding ~40 TB of storage per year

• Individual and institutional volunteers

• But where did the data go? Don't we need it anymore? Yes, but note that losing historical data is not a risk to the protocol - only to a single application. The job of the Ethereum core protocol, then, should not be to maintain all consensus data forever.

• So, who will store it? Here are some potential contributors:

• Individual and institutional volunteers

• Block explorers (e.g. etherscan.io), API providers and other data services

• Third-party indexing protocols like TheGraph can create incentivized markets where clients can pay servers for historical data as well as Merkle proofs

Clients in the Portal Network (currently under development) can store random parts of the chain history, and the Portal Network will automatically direct data requests to the node that owns it

BitTorrent, for example. A 7 GB file is automatically generated and distributed daily containing the blob data from the block

Application-specific protocols such as Rollup can require their nodes to store portions of history relevant to their application

The long-term data storage problem is a relatively simple one because of the 1 of N trust assumption we discussed earlier. We are still many years away from being the ultimate limit to blockchain scalability.

weak stateless

Ok, so we've handled history management pretty well, but what about state? The state problem is actually the main bottleneck in improving the TPS of Ethereum at present.

Full nodes take the pre-state root, execute all transactions in the block, and check that the post-state root matches what they provided in the block. To know whether these transactions are valid, they currently need state at hand - verification is stateful.

Enter the stateless era - we won't need state to function. Ethereum is striving for "weakly stateless", meaning that no state is required to validate blocks, but state is required to build blocks. Validation becomes a pure function - give me a completely isolated block and I can tell you if it works. Basically something like this:

• Because of PBS, it is acceptable for builders to still need state - they will be more centralized high-resource entities anyway. Focus on decentralized validators. Weak statelessness creates more work for builders and much less work for validators. This is a great tradeoff.

• You achieve this magical stateless execution with witnesses. These are proofs of correct state access that builders will start including in each block. You don't actually need the entire state to validate a block - you only need the state that was read or affected by the transactions in that block. Builders will start including the piece of state affected by the transaction in a given block, and they will prove that they correctly accessed that state via a witness.

• Let's take an example. Alice wants to send 1 ETH to Bob. To validate a block with this transaction, I need to know:

• Before transaction - Alice has 1 ETH

Alice's public key - so I can know the signature is correct

Alice's nonce - so I can know transactions were sent in the correct order

• After executing the transaction - Bob gained 1 ETH, Alice lost 1 ETH

• In a weakly stateless world, builders add the aforementioned witness data to blocks and attest to its accuracy. Validators receive the block, execute it, and decide whether it is valid. That's all!

• Here's what it means from a validator's perspective:

Gone is the huge SSD requirement for holding state - a critical bottleneck for scaling today.

Since you are now also downloading witness data and attestations, there will be an increase in bandwidth requirements. This is the bottleneck of the Merkle-Patricia tree, but it is moderate, not the bottleneck of Verkle's attempt.

Verkle Tries

You still perform transactions to fully validate. Statelessness acknowledges that this is not currently a bottleneck in scaling Ethereum.

Weak statelessness also allows Ethereum to relax its self-imposed constraints on execution throughput, and state bloat is no longer a pressing concern. It may be reasonable to increase the gas limit by a factor of about 3.

Most user execution will be on L2 anyway, but higher L1 throughput is still beneficial even for them. Rollups rely on Ethereum for DA (publishing to shards) and settlement (requires L1 execution). As Ethereum expands its DA layer, the amortized cost of issuing proofs will likely become a larger share of Rollup costs (especially for ZK-rollups).

We gloss over how these testimonies actually work. Ethereum currently uses Merkle-Patricia trees to represent state, but the required Merkle proofs are too large to be practical for these witnesses.

Ethereum will turn to Verkle to attempt state storage. Verkle proofs are much more efficient, so they can be weakly stateless as viable witnesses.

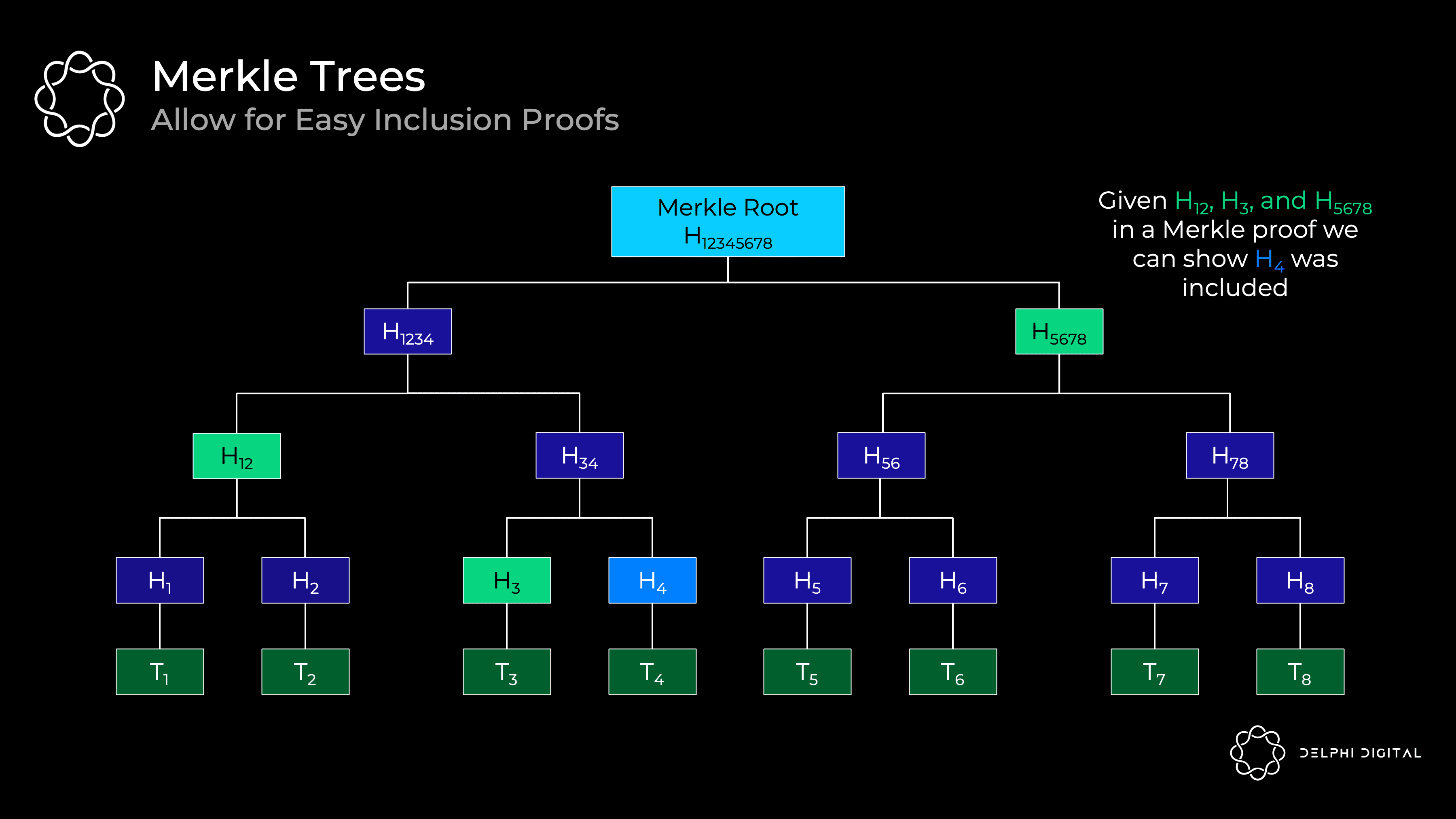
First let's review what a Merkle tree looks like. Every transaction is hashed - these hashes at the bottom are called "leaves". All hashes are called "nodes", which are the hashes of the two "children" nodes below them. The resulting final hash is the "Merkle root".

This is a useful data structure for proving contained transactions without downloading the entire tree. For example, if you want to verify that transaction H4 is included, you only need H12, H3, and H5678 from the Merkle proof. We have H12345678 from block header. Thus, a light client can ask a full node for these hashes, which are then hashed together based on the route in the tree. If the result is H12345678, then we have successfully proved that H4 is in the tree.

However, the deeper the tree, the longer the path to the bottom, so you'll need more items to prove it. Thus, shallow and wide trees seem to be favorable for efficient proofs.

The problem is that if you try to make the Merkle tree wider by adding more children under each node, it will be very inefficient. You need to hash all siblings together to climb the tree, so you need to receive more sibling hashes for Merkle proofs. This will make the proof size huge.

This is where efficient vector promises come in. Note that the hashes used in Merkle trees are actually vector commitments - they're effectively just commits to only two elements. So we want vector commitments, we don't need to receive all siblings to verify it. Once we have that, we can make the trees wider and reduce their depth. This is how we get effective proof size - reducing the amount of information that needs to be provided.

A Verkle trie is similar to a Merkle tree, but it uses efficient vector commitments (hence the name "Verkle") instead of simple hashes to commit to its children. So the basic idea is that each node can have many children, but I don't need all of them to verify the proof. It is a proof of constant size regardless of width.

In fact, we've covered a good example of one of these possibilities before - KZG commitments can also be used as vector commitments. In fact, this is what the ethereum developers originally planned to use here. They have since turned to Pedersen to undertake similar duties. These will be based on elliptic curves (Bandersnatch in this case), and they will each submit 256 values ​​(much better than two!).

So why not have the widest possible depth tree? This is great for validators who now have super compact proofs. But there is a practical trade-off that the prover needs to be able to compute the proof, and the wider it is the harder it gets. Therefore, these Verkle attempts will lie between the extremes that are 256 values ​​wide.

status expires

Weak statelessness removes the state inflation constraint for validators, but state doesn't magically disappear. Transaction costs are limited, but they impose a permanent tax on the network by increasing state. State growth remains a permanent drag on the network. Something needs to be done to fix the underlying problem.

This is where the state expires. Long periods of inactivity (like a year or two) are even cut from what block builders need to carry. Active users won't notice anything, and useless state that is no longer needed can be discarded.

If you need to restore the expired status, you just need to show a proof and reactivate it. This goes back to the 1 of N storage assumption here. As long as someone still has the full history (block explorers, etc.), you can get what you need from them.

Weak statelessness weakens the immediate need for state expiration at the base layer, but is a good thing in the long run, especially as L1 throughput increases. This would be a more useful tool for high-throughput rollups. L2 state will grow at an order of magnitude higher rate, dragging down even high-performance builders.

• Part III - MEVs

• PBS is necessary for the secure implementation of DS, but recall that it was actually originally designed to combat the centralized power of MEV. You’ll notice a recurring trend in Ethereum research today — MEV is now front and center in cryptoeconomics.

Designing a blockchain with MEV is critical to maintaining security and decentralization. The basic protocol-level methods are:

Minimize harmful MEV as much as possible (e.g. single slot finality, single secret leader election)

Democratize the rest (e.g. MEV-Boost, PBS, MEV smoothing)

The rest must be easily captured and propagated among validators. Otherwise, it centralizes the validator set since it cannot compete with complex searchers. This is exacerbated by the fact that combined MEV will have a higher share of validator rewards (staking issuance is much lower than the inflation rate given to miners). Can not be ignored.

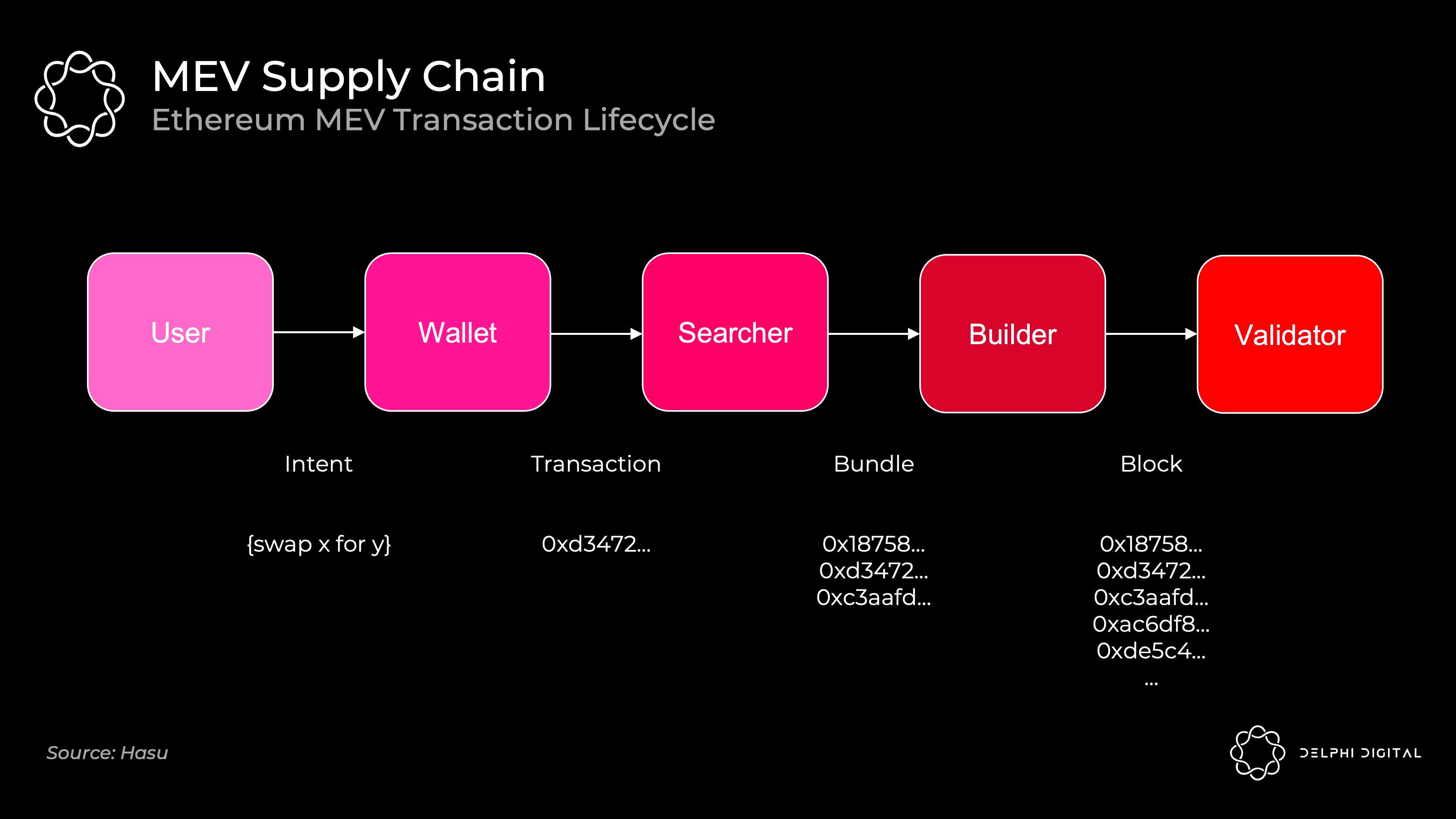
Today's MEV supply chain

Today's sequence of events is as follows:

MEV-Boost

Mining pools play the role of builders here. MEV Seekers relay transaction bundles (and their respective bids) to pools via Flashbot. The mining pool operator aggregates a complete block and passes the block header to the individual miners. Miners prove this by giving them weight in the fork selection rules through PoW.

Flashbots are here to prevent the vertical integration of the entire stack - which would open the door to censorship and other nasty externalities. When Flashbots came out, mining pools had already started striking exclusive deals with trading companies to extract MEV. Instead, Flashbots gave them an easy way to aggregate MEV bids and avoid vertical integration (by implementing MEV-geth).

After the merger of Ethereum, the mining pool will disappear. We want to open the door for validator nodes that can reasonably function at home. This requires finding someone to fill a dedicated build role. Your home validator node may not be as good at capturing MEV as a hedge fund with quantized salaries. Left unchecked, this will centralize the validator set if ordinary people cannot compete. If properly structured, the protocol could redirect MEV revenue to daily validator staking rewards.

Unfortunately, the PBS within the agreement simply wasn't ready for the merger. Flashbots again offers a stepping stone solution - MEV-Boost.

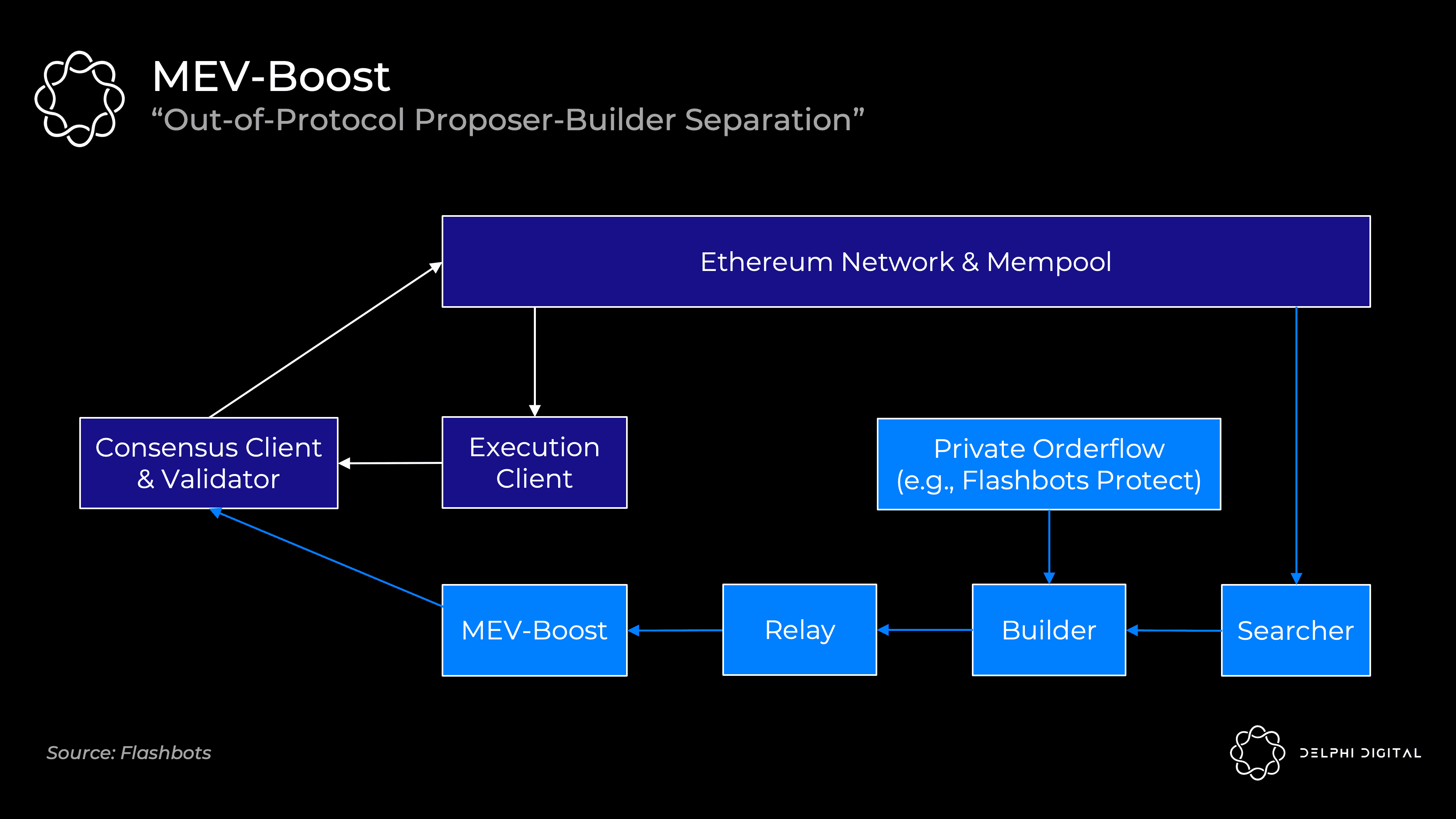
Merged validators will by default receive public mempool transactions directly into their execution clients. They can package these up, give them to consensus clients, and broadcast them to the network. (If you need to understand how Ethereum's consensus and execution clients work together, I'll cover that in Part IV).

But as we discussed, your validators don't know how to extract MEV, so Flashbots offer another option. MEV-boost will plug into your consensus client, allowing you to outsource specialized block building. Importantly, you still have the option to use your own execution client as a fallback.

MEV Seekers will continue to function in the same way they do today. They will run specific strategies (statistical arbitrage, atomic arbitrage, sandwiches, etc.) and bid on their bundles. Builders then aggregate all bundles they see, as well as any private order streams (e.g., from Flashbots Protect) into the best full block. Builders only pass block headers to validators via a relay running to MEV-Boost. Flashbots intends to run relayers and builders, and plans to decentralize over time, but it may be slow to whitelist other builders.

MEV-Boost requires validators to trust relayers - the consensus client receives the block header, signs it, and only then displays the block body. The purpose of the relayer is to prove to the proposer that the body is valid and exists, so that the verifier does not have to trust the builder directly.When the in-protocol PBS is ready, it will incorporate content provided by MEV-Boost during that time. PBS provides the same separation of powers, allowing for easier builder decentralization and removing the need for proposers to trust anyone.。

Committee-driven MEV smoothing

PBS also opened the door for another cool idea --

Committee-driven MEV smoothing

We see that the ability to extract MEV is a centralizing force for the validator set, but so is the distribution. The high variability in MEV rewards from block to block motivates pooling many validators to smooth your rewards (as we see with mining pools today, though to a lesser extent here).

The default is to provide the actual block proposer with the builder's full payment. MEV smoothing will instead distribute the payment among many validators. A committee of validators will check the proposed block and certify if this is indeed the block with the highest bid. If all goes well, the block proceeds and the reward is split between the committee and the proposer.

This also solves another problem - out-of-band bribery. For example, proposers could be incentivized to submit suboptimal blocks and accept out-of-band bribes directly to hide their payments from delegators. This proof can check the proposer.

In-protocol PBS is a prerequisite for MEV smoothing. You need to understand the builders market and the clear bids submitted. There are several open research questions here, but this is an exciting proposal that is again critical to ensuring decentralized validators.

Single slot transaction finality

Fast finality is great. Waiting ~15 minutes is not optimal for UX or cross-chain communication. More importantly, this creates a MEV reassembly problem.

The merged Ethereum already provides stronger confirmation than today - thousands of validators attesting to each block competing with miners and possibly mining at the same block height without voting. This would make reorganization highly unlikely. However, this is still not true transaction finality. If the last block had some fat MEV, you might just trick the validators into trying to reorganize the chain and steal it for themselves.

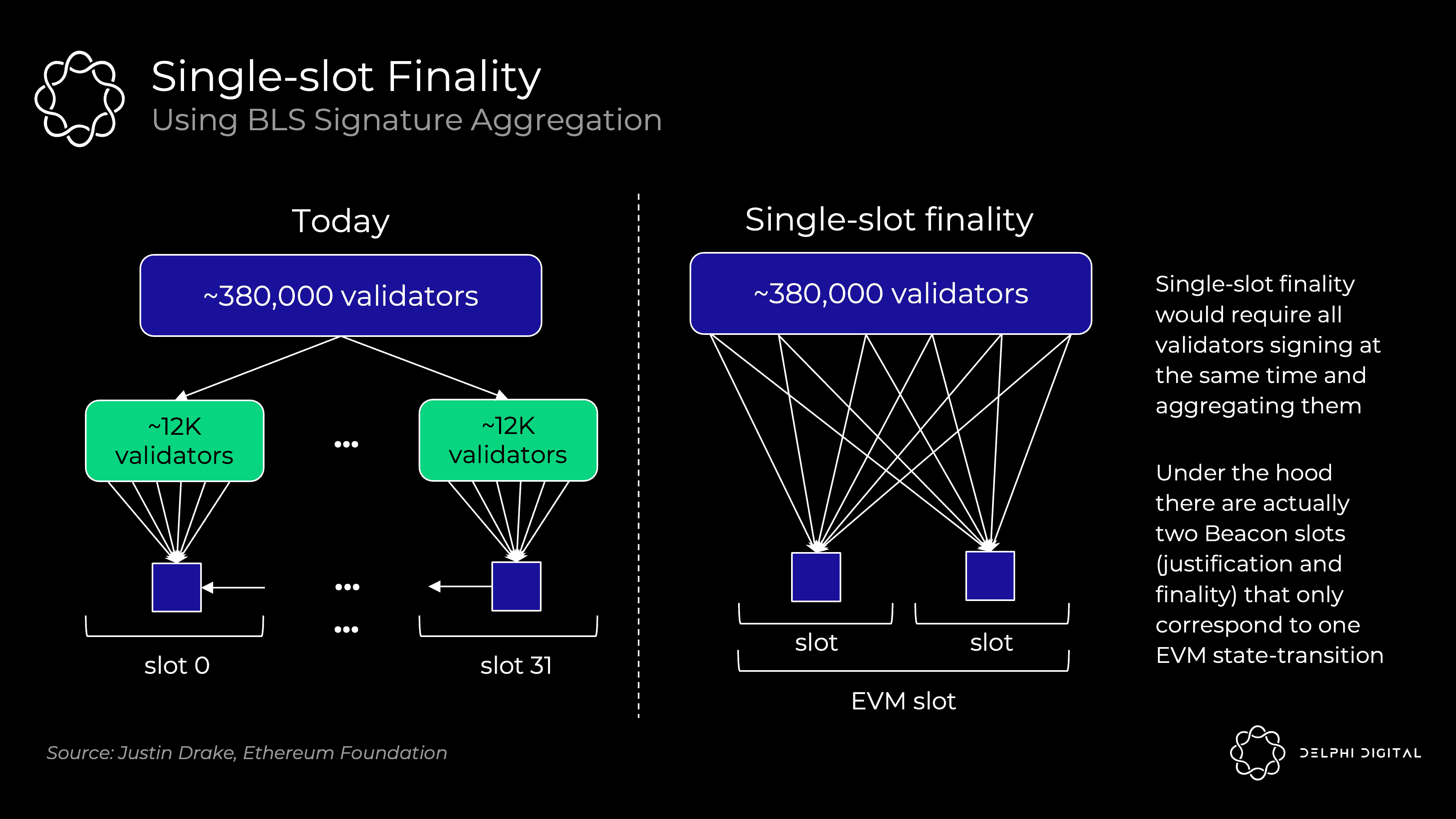
I wouldn't dwell too much on the underlying mechanics here. Single slot finality has been developed very far in the roadmap of Ethereum, and it is a very open design space.hereIn today's consensus protocol (without slot finality), Ethereum only needs 1/32 of validators to attest to each slot (about 12,000 out of about 380,000 currently). Extending this kind of voting to a full validator set aggregated with BLS signatures in a single slot would require more work. This condenses hundreds of thousands of votes into a single validation:

Vitalik is at

here

Breaks down some interesting solutions.

Single Secret Leader Election (SSLE)

SSLE attempts to patch another MEV attack vector that we will face after the merger.

The list of beacon chain validators and the list of upcoming leader elections are public, and it is easy to deanonymize them and map their IP addresses. You can probably see the problem here.

More sophisticated validators can use tricks to hide themselves better, but small validators are especially vulnerable to doxxed and subsequent DDOSd. This can be easily used for MEV.

Suppose you are the proposer of block n and I am the proposer of block n+1. If I know your IP address, I can cheaply DDOS you so that you time out and fail to generate your blocks. I can now capture our slot's MEV and double my rewards. This is exacerbated by EIP-1559's elastic block size (maximum gas per block twice the target size), so I can cram transactions that should have been two blocks into my now twice as long in a single block.

Part IV - Merger

The merged client

Well, just to be clear I was joking. I actually think (hope) that the Ethereum merger happened relatively quickly.

• We're all talking about this topic, so I feel obligated to at least give it a brief introduction.

• The merged client

Today, you run a monolithic client that handles everything (e.g. Go Ethereum, Nethermind, etc.). Specifically, full nodes simultaneously perform the following operations:

Execution - Every transaction in the block is executed to ensure validity. Get the pre-state root, perform all operations, and check that the resulting post-state root is correct

Consensus - Verify that you are on the heaviest (highest PoW) chain that gets the most work done (i.e. Satoshi Consensus)

• They are indivisible because full nodes follow not only the heaviest chain, but also the heaviest valid chain. That's why they are full nodes and not light nodes. Even if a 51% attack occurs, the full node will not accept invalid transactions.

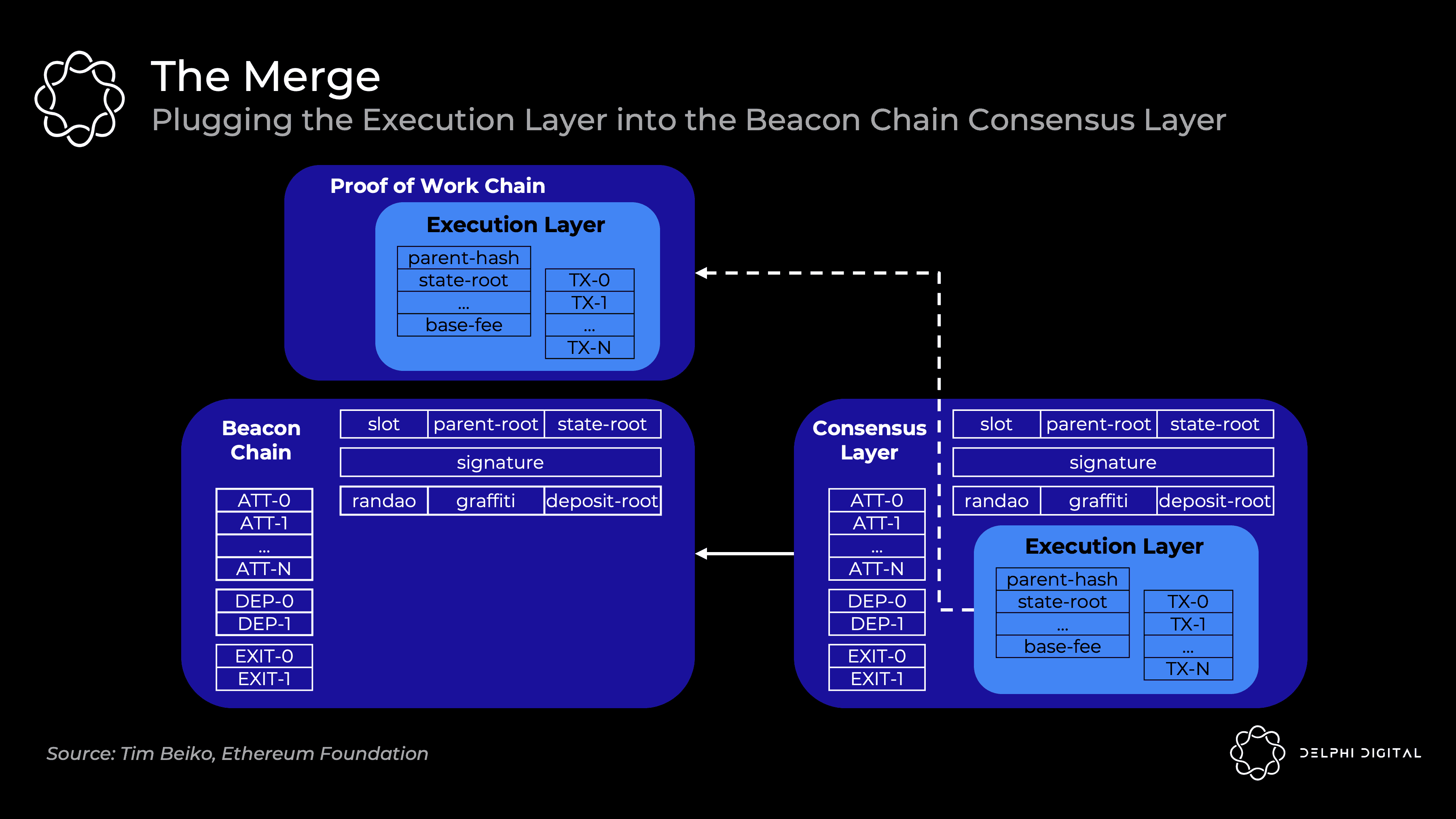
• The beacon chain is currently only running consensus to give PoS a test run. Execution is not included. The final total difficulty will eventually be determined, at which point the current Ethereum execution block will be merged into the beacon chain block to form a chain:

However, a full node will run two separate clients in the background, which can interoperate:

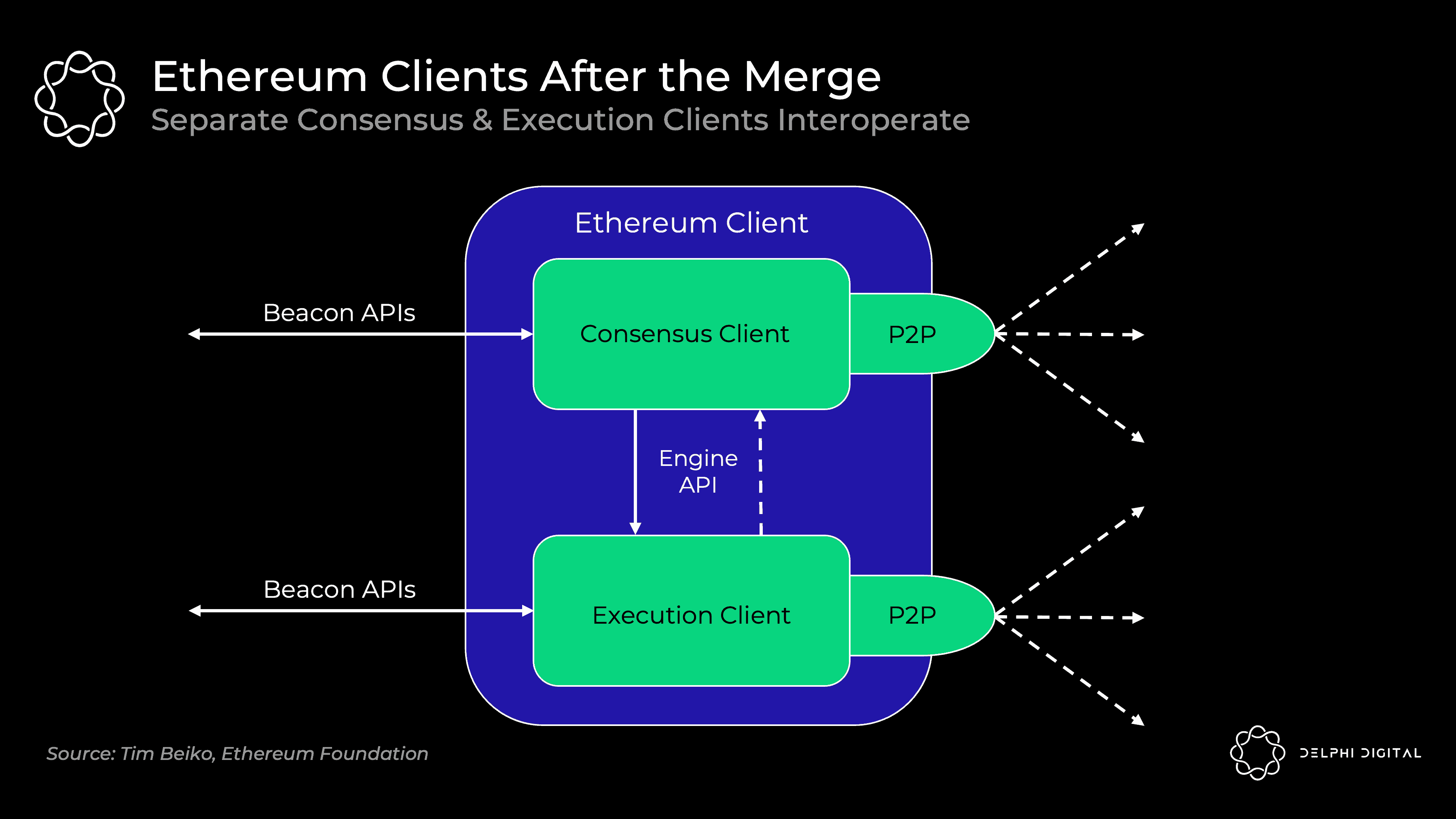
Execution Client (aka "Eth1 Client") - The current Eth 1.0 client continues processing execution. They process blocks, maintain memory pools, manage and synchronize state. The PoW part was ripped out.

Consensus Client (aka "Eth2 Client") - The current beacon chain client that continues to process PoS consensus. They keep track of the head of the chain, gossip and attest to blocks, and earn validator rewards.

Clients receive beacon chain blocks, execute client run transactions, and if all goes well, consensus clients follow the chain. You will be able to mix and match the execution and consensus clients of your choice, all of which will be interoperable. A new engine API will be introduced for clients to communicate with each other:

or:

post-merger consensus

The merged Ethereum moved to GASPER - a combination of Casper FFG (finality tool) and LMD GHOST (fork choice rule) for consensus. TLDR here - it's a liveness that favors consensus, not security.

in conclusion

The difference is that security-friendly consensus algorithms (e.g., Tendermint) stop when they fail to obtain the requisite number of votes (here set to 2/3 of the validators). Favorable chain liveness (e.g., PoW + Nakamoto consensus) will continue to build an optimistic ledger anyway, but they cannot reach finality without enough votes. Bitcoin and Ethereum today are never finalized - you just assume that reorgs won't happen after a sufficient number of blocks.

However, Ethereum will also achieve finality through regular checkpoints with enough votes. Each 32 ETH instance is a single validator, and there are already over 380,000 beacon chain validators. Epochs consist of 32 slots where all validators split and attest a slot within a given epoch (meaning ~12,000 proofs per slot). The fork selection rule LMD Ghost then determines the current head of the chain based on these proofs. A new block is added every slot (12 seconds), so the epoch is 6.4 minutes. Finality is usually achieved after two epochs (that is, 64 slots, although up to 95 may be needed) with the necessary votes.