
This is part 2 of our Polkadot Consensus series.
In this introduction to the series, a consensus algorithm is outlined that can help computer networks answer three questions. GRANDPA will address the second problem.
1. Who can propose the next change?
2. Which set is the final change?
3. What if someone breaks the rules?
GRANDPA is the final tool of Polkadot, its role is to correctly select the model chain, indicating that a series of changes to GRANDPA is the final step. GRANDPA will not generate blocks on its own; instead, GRANDPA validators will import blocks from another block producing component (which we will discuss in Part 3).
secondary title
GRANDPA agreement
GRANDPA differs from other Byzantine Fault Tolerant (BFT) blockchain algorithms in that validators vote on chains rather than blocks. The protocol adopts a transitional voting mechanism, and the GRANDPA algorithm finds the block number with the highest number of votes, which will be regarded as the final vote. This process allows for several blocks to take place simultaneously.
That last part is important because GRANDPA removes a bottleneck that has held back other blockchain finalization tools. Like other PBFT derivatives of Practical Byzantine Fault Tolerance, GRANDPA has O(n²) complexity. That is, if you double the number of nodes, you must send four times the number of messages. A consensus system that makes block production part of the deterministic process allows you to send these messages to each block. By isolating block production in another module, we can produce blocks in a more efficient manner (O(n) for BABE), and finalize several of them in one round of voting.
To understand this example, look at the following log messages from the Kusama node:
Idle (24 peers), best: #664257 (0x706c…76b7), finalized #664253 (0xe4ab…4d2a)
Imported #664258 (0xee71…6321)
Idle (24 peers), best: #664258 (0xee71…6321), finalized #664256 (0x809a…a5d8)
Note that in one round, GRANDPA finalized three blocks (664,254 to 664,246).
secondary title
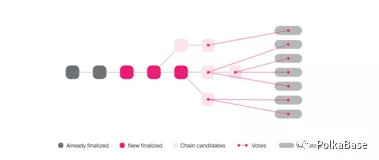
A GRANDPA round
Voters will do the following to generate new blocks:
1. The node designated as the "primary" will broadcast the block with the highest votes it believes may have been obtained before as the final block.
2. After waiting for a network delay, each validator broadcasts a "pre-vote" for the highest-voted block it believes should be finalized and considered final. If the majority of validators are honest, this block should extend the originally broadcast chain. So the new chain may be several blocks longer than the finalized chain.
3. Each verifier can determine the final block with the highest votes according to the pre-voting calculation. If the pre-vote set extends to the last finalized chain, each validator will "pre-execute" that chain.
4. Each validator waits to receive enough pre-executions to deliver information on the newly determined chain.
A subtle but important difference from other Byzantine Fault Tolerant algorithms such as PBFT and Hotstuff is that there are no opinion changes on the critical path of this voting round. Although the main content of each round is changed, this change only starts a new round in an asynchronous network, so in a partially synchronous network, even if no main land is assigned, the protocol will always move forward.
When more than two-thirds of the verifiers' pre-vote or pre-execution is obtained in the protocol process, it indicates that the process can be completed. To achieve finality, the number of votes in a validator's hand must be limited, unlike chains which can have infinite validator set finality. The method of selecting the set of voters is logic defined outside of the GRANDPA protocol (see Section 4).
secondary title
Safety Responsibilities: When the Accident Happens
GRANDPA has a feature called Security Accountability that makes validators accountable for security breaches. When a security conflict occurs when two blocks in different chains are determined, the security responsibility function is similar to an investigation after an accident.
But first it is clear how the two conflicting chains are formed? BFT systems are always built on the condition that the maximum number of validators in question is a small fraction (in our case a third) of the total validators. If the validator set fails to meet the above requirements, at least one-third of the validators vote for both chains in order to finally clear the two conflicting chains.
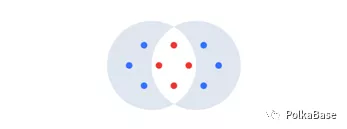
In this example, there are 10 validators, which means that 3 is the maximum number of false validators the system can tolerate (f = (10-1)/3). With 4 bad validators (red) and a network partition, each set of honest validators (blue) can have their respective blocks final.
Voting on two conflicting chains is an ambiguous act. In fact everyone thinks that ambiguity is an attack on BFT systems, but in GRANDPA we can detect this behavior.
First, we will ask why nodes voted for a new block without considering the previous block. Any honest validator should enable a second set of pre-votes or pre-executions to answer this question, since the second block will always have the majority of votes.
If the first question is true, then we ask the second question: which ballots from the first round did you see? We are essentially asking them to approve other validators and disclose all the votes they have received from their peers. Somewhere in the union of these two sets, you'll find the validators who voted for the two conflicting chains. Once the above results are confirmed, they will be heavily penalized, but this is only the result of on-chain logic work and not consensus.
secondary title
How GRANDPA Achieves Usability and Effectiveness
Remember the log message above? Note that the final block is the second block after the best block. This lag is actually an advantage in keeping block production and completion different.
Idle (24 peers), best: #664258 (0xee71…6321), finalized #664256 (0x809a…a5d8)
Blockchain interoperability systems, including Polkadot, have issues with data availability. Imagine a collator committing a block to a validator, but none of the other parachain collators see it. What if the collector who submitted the block information goes offline? Validators are responsible for helping to store complete block information for a period of time so that all parachain collectors can obtain block information.
Validators are supposed to validate block candidates before voting on them, but we want to make sure they do. In Polkadot there are many nodes known as phishers who can validate blocks and report misbehavior by validators, such as pointing out an invalid parachain in the relay chain.
We never want the final selected block to be an invalid block or a block that the collator cannot reconstruct. By keeping the verifiability of several blocks behind the end of the chain, we can allow the phishers to verify that the block is correct and verify that the verifier is conscientious.
Original link:
Original link:https://polkadot.network/polkadot-consensus-part-2-grandpa/
Translation / Mike
Edit / Dolly