Original title: "Price Oracle for Derivative Assets" (Price Oracles for Derivative Assets）

Author: Jonathan Erlich

Original compilation: 0 xStephen

1 Introduction

In this post, we analyze existing assumptions about oracles for derivative asset prices in the context of DeFi lending protocols. Specifically, we discuss why using the price of an underlying asset as a price feed for a derivative is generally a bad practice that should be avoided. Given the prevalence of this practice, we believe this is a timely and important question.

We will focus on two types of derivative assets: cross-chain assets and liquid collateralized derivatives. However, a similar analysis can be generalized for any type of derivative asset.

This article is divided into three parts: cross-chain assets, liquidity-backed derivatives, and concluding thoughts.

2. Cross-chain assets

When a derivative asset is priced using the underlying asset as a proxy, there is an underlying assumption (or at least an assumption implicit in the decision) that the two assets will follow the same price trajectory over time. And generally, this is the case.

If everything is working properly, the price of the underlying asset should closely track the price of the derivative. However, this assumption can be broken when things don’t go as expected, which happens quite often in the case of cross-chain assets. Let's explore an example to understand why.

Suppose we have bridgedETH, the cross-chain version of ETH on different L 1 chains. Under normal circumstances, each bridgedETH is backed by ETH locked in one of Ethereum's smart contracts (pegged based on a 1:1 ratio). However, these normal situations do not always hold. In particular, as has happened several times, cross-chains can be exploited, resulting in the theft of underlying assets. As an example, let's assume this is exactly what happened to our bridgedETH, the attacker exploited the cross-chain and was able to steal all the ETH backing bridgedETH.

So, how will this affect lending protocols that use the ETH price as a proxy for bridgedETH? Fundamentally, this means that the protocol values ​​each bridgedETH at 1 ETH, while its true price is 0 ETH (assuming this is also its market price). This leaves the protocol with the following loopholes:

• It allows attackers to steal funds from the protocol using bridgedETH as collateral. Any attacker can buy bridging ETH from the market for 0, deposit it as collateral to the protocol (where it is worth 1 ETH, and borrow (steal) other Assets. This type of attack has been used on different real-time protocols (for example, against Hundred Finance on Moonriver and Aave on Harmony).

• It prevents liquidation from working properly. When the market price of bridgedETH drops from 1 ETH to 0 ETH, some positions using bridgedETH as collateral should become liquidable. However, these positions will not be liquidable given that the protocol still values ​​each bridgedETH at 1 ETH. Whether these positions will actually be liquidated if a powerful oracle is used is another interesting question, and will ultimately depend on how quickly the market price of bridgedETH falls. However, such an analysis is outside the scope of this article. The important point is that under the fragile oracle mechanism, these positions will not even become bad debts that can be liquidated.

As a potential solution to this problem, Aave is considering hooking into Chainlink's Proof-of-reserve price feed. On a macro level, these price feeds will allow Aave to verify that the underlying assets that support cross-chain derivatives actually exist. While this may be a viable solution, the details of its implementation are still too sparse to allow a full assessment. Also, this solution doesn't handle some special cases well.

For example, the underlying asset may become inaccessible or "expired," which means a bug in the contract locks the underlying asset in the contract forever. In this case, the underlying assets actually exist, so there will be no proof of reserve issues. However, derivatives are worthless if the underlying asset cannot be recovered. Market prices will likely reflect this, which would leave the protocol with the loopholes explored above. While this is a low-probability event, it should be considered when evaluating solutions.

3. Liquid Collateralized Derivatives (LSD)

When using the price of the underlying asset as a proxy for the derivative asset, LSD is subject to the same vulnerabilities as cross-chain assets. Given that we've covered these issues in the previous section, let's look at a more complex case in DeFi specifically for LSD.

Before getting into specifics, it's worth briefly discussing how LSD works. As its name suggests, LSD is a liquid proof of collateral underlying assets (usually in PoS networks). In this case, the liquidity staking protocol works as follows:

• It receives assets to be staked from the user side

• It delegates these assets to some validators (nodes)

• It returns to the user a proof (negotiable) of the mortgaged asset: ie LSD

When a user wants to withdraw the underlying asset (exchange LSD for a circulating asset), the protocol works as follows:

• It receives LSD from user side

• It uses the redemption rate to figure out how much of the underlying asset should be returned to the user. The redemption rate is the ratio of the LSD supply to the underlying asset (ie it indicates how much of the underlying asset each LSD represents).

• It unstakes the necessary underlying assets

• After the release period, users can claim assets

With this background, let's return to the question of price. The current method used by some agreements to calculate the price of LSD is to take the price of the underlying asset and the redemption rate into consideration. The calculation method is as follows:

in:

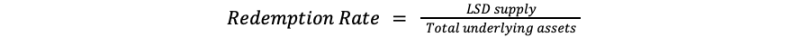
By incorporating the redemption rate into the calculation, this approach addresses the situation explored in the previous section, where the underlying asset could be stolen (or slashed in the case of a PoS protocol). For example, if the underlying asset is stolen, it will be reflected in the redemption rate, and therefore, the price will also be affected.

So, what's wrong with this approach? Let us explore this issue with the following example. In this example, assume we have an LSD of ATOM called stakedATOM that works in a similar way to the LSD we described above, and has a 21-day release period. Using the pricing method described above, the price of stakedATOM is calculated as follows (assuming we denominate in USD):

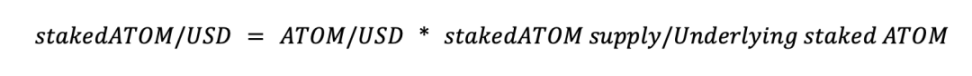
in:

There is a fundamental problem with this approach: the actual market price of stakedATOMs may differ from the calculated price discussed above. This is because, while an arbitrage opportunity exists when the market price of stakedATOM is higher than the calculated price, this is not the case when the price of stakedATOM is lower than the calculated price.

In other words, while the market price of stakedATOM has a hard peg (equivalent to the calculated price) on the upside, it does not exist on the downside. To understand why, let's explore how the arbitrage opportunity works in both cases. The rise is as follows:

• Suppose the redemption rate is 1 ATOM/stakedATOM.

• The market price is 1.1 ATOM/stakedATOM (stakedATOM is overvalued in the market).

• An arbitrageur can stake 1 ATOM, receive 1 stakedATOM, and then sell the stakedATOM in the market for a profit of 0.1 ATOM.

The above happens until the arbitrage opportunity no longer exists. This mechanism guarantees that the market price will tend to have an upper bound equal to the calculated price. However, this is not the case when the price is down, because the 21-day release period breaks the arbitrage opportunity. Here is another example:

• Suppose the redemption rate is 1 ATOM/stakedATOM.

• The market price is 0.9 ATOM/stakedATOM.

• If there is no release period, arbitrageurs can use 0.9 ATOM to buy 1 stakedATOM in the market and release the pledged ATOM to get back 1 ATOM, with a profit of 0.1 ATOM.

• However, the release period is 21 days, so there is no immediate arbitrage opportunity.

So, there is a "hard peg" for price increases, but a "soft peg" for price drops. This soft peg means that, in the long run, market prices should tend to follow the redemption rate. But in the short term, the price of stakedATOM does not have a real floor. This is not just a theoretical or abstract finding, in reality we have seen this, for example with the infamous stETH unpegging event and other LSDs such as stLUNA. Basically, when enough people want to claim LSD without waiting for the release period, the price tends to "decouple" downwards.

For lending protocols that use the calculated price as an oracle feed for LSD, the above volatility could lead to insolvency. Let's take a look at the following example to understand how this happens:

Suppose we have the following positions in the DeFi lending agreement:

• A user deposits 100 stakedATOMs as collateral with a maximum loan rate of 70%

• The user lent $600 worth of other assets using stakedATOM as collateral

Now let's explore how the position changes in the T 1, T 2 and T 3 time nodes in the following diagram:

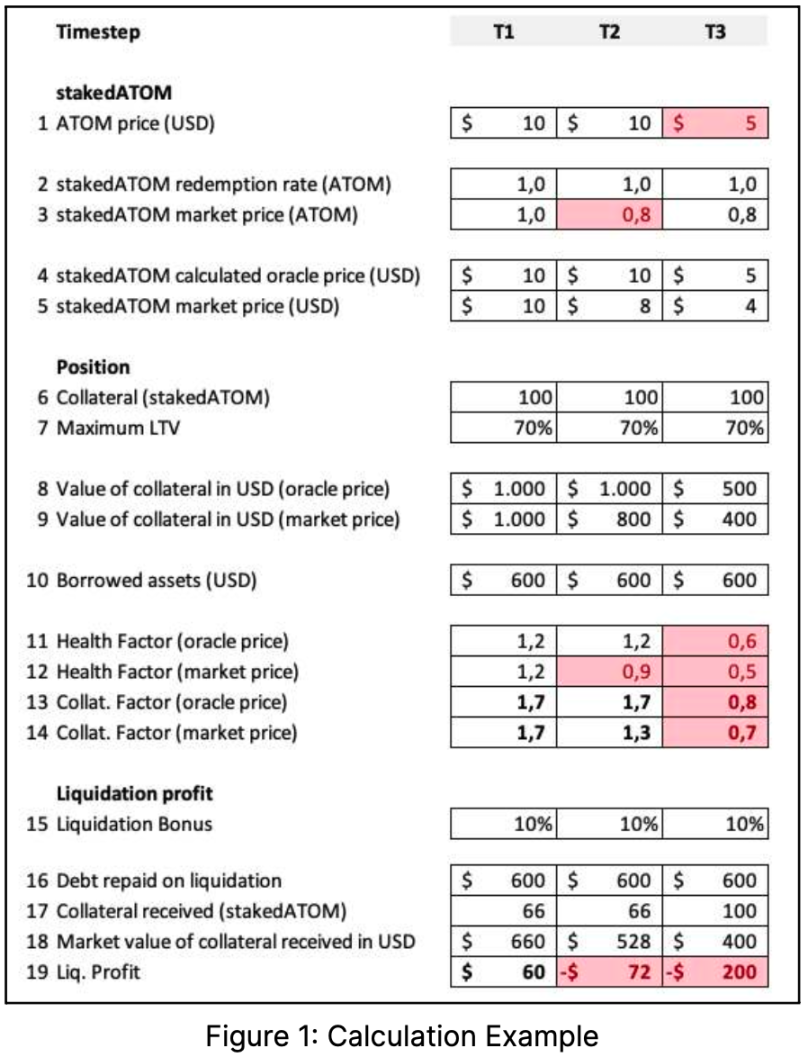
At T 1, the market price of stakedATOM (line 4) perfectly mirrors the calculated oracle price (line 5), so everything is running smoothly; specifically, the health factor (Collateral*Max. LTV/Debt) and the collateral coefficient (Collateral/Debt) are both higher than 1, so the account is healthy and over-collateralized;

In T 2, the market price of stakedATOM deviated from the redemption rate (and thus from the oracle price). Specifically, although the redemption price is 1 ATOM, the market price is 0.8 ATOM (with a 20% deviation); there are several parts worth elaborating on in this case:

• The health factor (line 12) calculated with the market price of stakedATOM is no longer above 1, meaning that the position measured with the market price is unhealthy and should be liquidable. However, given that the protocol is using the oracle price, and the oracle price has not changed, the health factor (line 11) calculated using the oracle price is still exactly the same as in T 1 and higher than 1. Therefore, the position cannot be liquidated.

• Note that at this point, liquidation of the position is no longer profitable for the liquidator (see last line). This is due to the agreement's calculation of what to pay to the liquidator based on the oracle's price. The amount of stakedATOM collateral, and the price of the oracle is overvalued. If the oracle is using market prices, then the position is liquidable, at which point liquidation is profitable.

• While this isn't ideal, it's not too bad considering that a position that should have been liquidated didn't because the position was still solvent. In other words, it is still overcollateralized (collateralization factor higher than 1).

In T3, the deviation between the market price and the redemption rate is the same as in T2, but the price of ATOMs is reduced from $10 to $5. This would effectively result in an insolvent position as it would not be liquidated and now the collateralization ratio has dropped below 1.

Fundamentally, the problem with this oracle approach is that even if everything goes according to plan and no price manipulation occurs, the system can become insolvent, as explored above.

4. Concluding Thoughts

Oracles are at the heart of DeFi lending protocols. They are so important that they often determine the future of the entire protocol. An unsound oracle can put millions of dollars worth of assets at risk, which is why we spend so much time analyzing oracle implementations.

Through this article, we hope to shed some light on the use of oracles for derivative assets. In particular, we have shown why some common practices are suboptimal and should be avoided. The purpose of this post is not to discourage the listing of derivative assets, as we know they are some of the best assets that can be used as collateral. Our intention is to discourage the listing of these derivative assets with less robust oracles, which could lead to the worst possible outcomes.

We know that derivative assets are often less liquid than their underlying assets, making it difficult to build robust oracles specifically for them. However, we don't think this should be an excuse to use non-robust oracles. We strongly encourage protocols to wait for liquidity to be established and asset-specific robust oracles to be developed before using non-robust oracles.