Original Author: Xiang|W3.Hitchhiker
Original editor: Evelyn|W3.Hitchhiker
 List of different polynomial commitment schemes
List of different polynomial commitment schemes
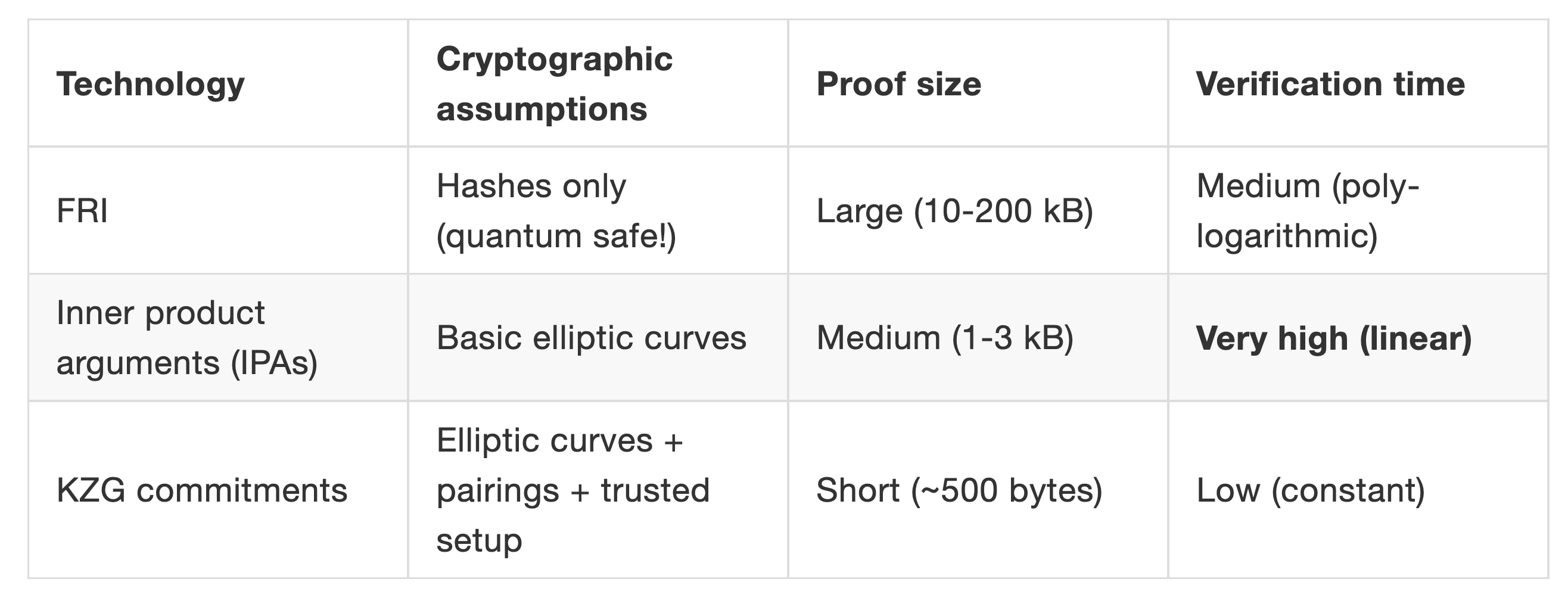
In the above table, FRI is the polynomial commitment scheme adopted by Starkware, which can achieve quantum-level security, but the amount of proof data is the largest; IPA is the default polynomial commitment scheme of Bulletproof and Halo2 zero-knowledge algorithms, and the verification time is relatively long. There are Monero, zcash, etc., and the first two do not require initial trusted settings.
It can be seen from the above figure that KZG polynomial commitment has a relatively large advantage in terms of proof size and verification time, and KZG commitment is also the most widely used polynomial commitment method at present. But KZG is based on elliptic curves, pairing functions, and requires initial trusted settings.
Linking ETH Upgrade Routes to Polynomial Commitments
secondary title
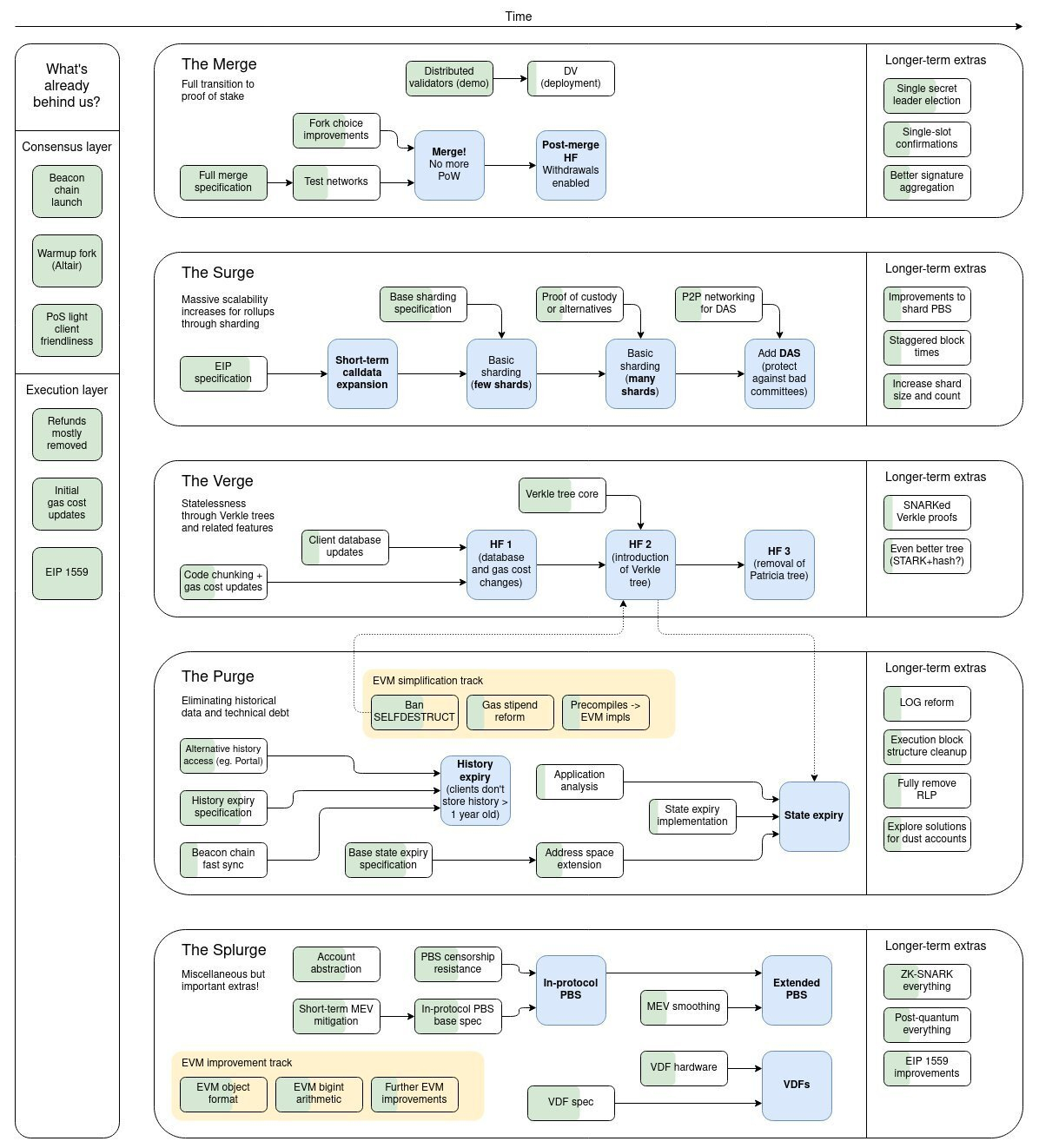
The Merge:
secondary title
The Surge:
secondary title
The Verge:
secondary title
The Purge:
secondary title
The Splurge:
The coordination of the four different parts after the upgrade aims to reduce the occurrence of errors (Bugs) and ensure the smooth operation of the network, as well as the improvement of EVM and the addition of account abstraction models.
Among them, The Surge upgrade will use polynomial commitment technology to achieve data sampling function, The Verge upgrade will use polynomial commitment to optimize its data structure, and ETH L2's zkrollup also uses polynomial commitment to achieve performance expansion brought by its zero-knowledge proof .
What is KZG Polynomial Commitment
This article only introduces the well-understood KZG polynomial commitment. KZG polynomial commitment (KZG Polynomial Commitment), also known as the Carter polynomial commitment scheme, was published by Kate, Zaverucha and Goldberg. In a polynomial scheme, the prover computes the commitment of a polynomial and can open it at any point in the polynomial. This commitment scheme can prove that the value of the polynomial at a specific position is consistent with the specified value.
It is called a commitment because when a committed value (a point on an elliptic curve) is sent to an object (the verifier), the prover cannot change the polynomial currently being computed. They can only provide a valid proof for a polynomial; when trying to cheat, they either fail to provide a proof or the proof is rejected by the verifier.
KZG Mathematical Principles
For details, please refer to what Dr. Qi Zhou explained in Dapp Learning aboutKZG video。
first level title

secondary title

single proof
Carter proves that the formula for a single data is deduced as follows. Since the elliptic curve group only supports additive homomorphism, it cannot support multiplication between polynomials. This needs to be solved by pairing functions.

Since the elliptic curve group does not support the multiplication operation between polynomials, it is necessary to use the pairing function to solve the problem.

batch proof
Specific application scenarios
The application direction of polynomial commitment can be summed up into three categories
Data availability (ETH Surge upgrade, ETH darksharding, L2 cost reduction, modular data availability project Avails)
Data structure optimization (MPT tree changed to Verkle tree, ETH Verge upgrade, stateless client, lightweight verification node for ETH)
Zero-knowledge proof system (Zksync, Zkswap, Scroll, PSE provide Zk with a polynomial commitment scheme, which greatly improves the chain’s expansion ability)
1. Data Availability
DAS (Data Availability Sampling)
Core purpose: If the data is missing, it will not pass the spot check of most nodes
Do our best: occupy less bandwidth, and require less computation during the sampling process
Erasure code (celestia)
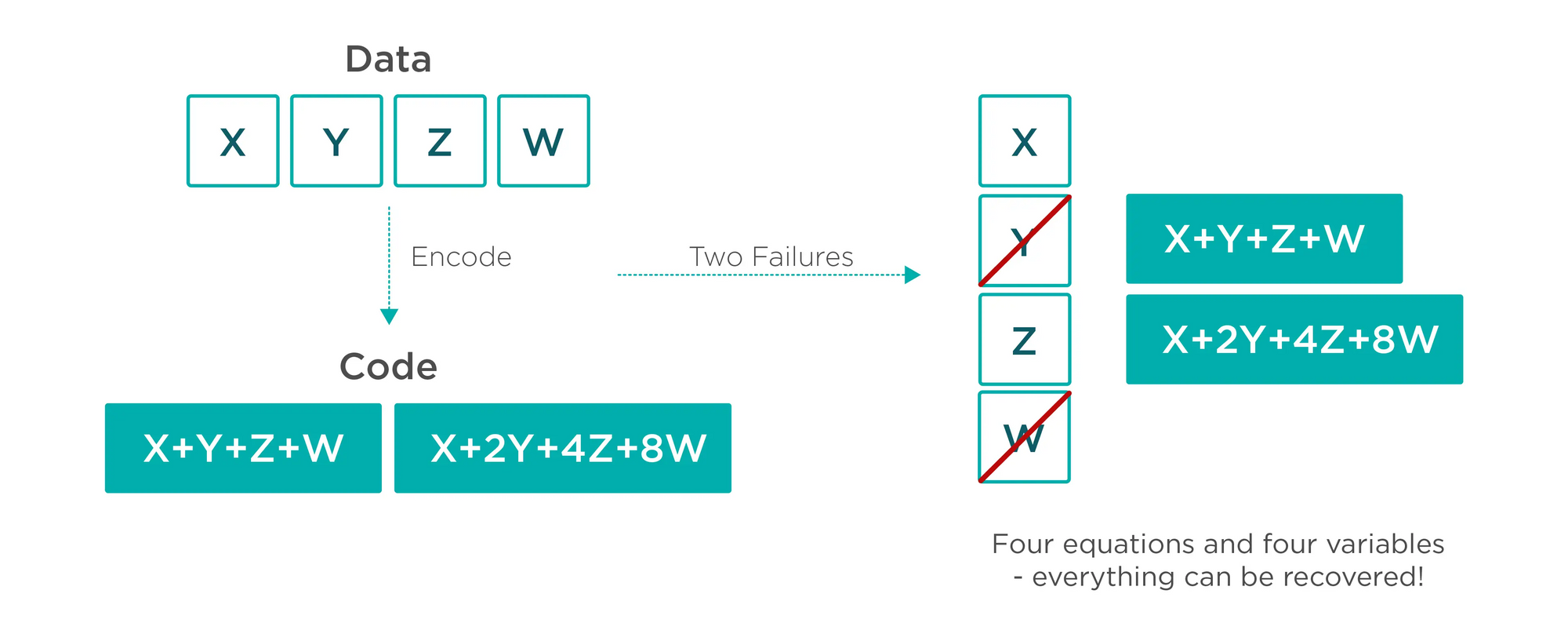
Erasure coding adds extra data blocks, which can be easily detected by spot investigation, thereby improving security.
Take the above picture as an example, there are 4 data, only one can be sampled at a time, assuming that there is a problem with one data, the probability that each user finds an error is 1/4, but after adding two data blocks, there is still a problem with one data, user sampling The probability of discovery can be as high as 1/2 (3/6). This greatly improves security.
KZG can also implement erasure codes, using the Lagrangian formula:
For example, put (0,3), (1,6) into the formula, y=3x+3
y1, y2 can be understood as the data to be saved,
Corresponding points (2,8) (3,12) and so on, where the y value can be used as erasure code data, and any two points can be derived from the coefficients of the original polynomial formula.
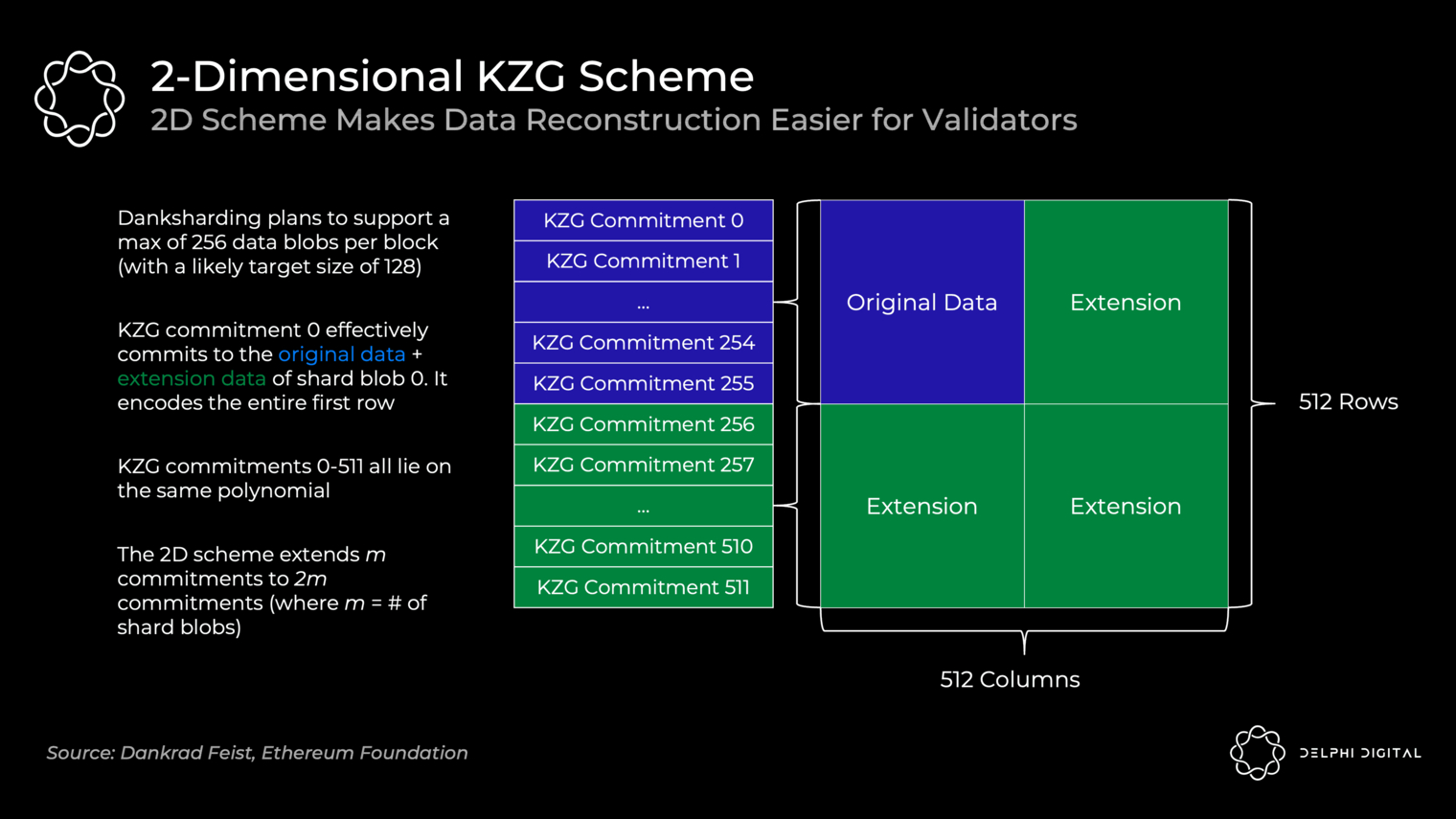
Composition of different data availability items
Celestia = Tendermint (cosmos) + 2d erasure code + fraud proof + Namespace merkle tree + IPFS infrastructure (IPFS Blockstore for data storage, Libp2p and bitswap of IPFS for transmission network, Ipld of IPFS for data model)
Polygon Avail = Substrate(Polkadot) + 2d erasure code + KZG polynomial commitment + IPFS infrastructure
ETHprotoDankSharding = Blobs data (storage for data availability, replace existing calldata) + 2d erasure code + KZG polynomial commitment (to be determined,planStill under discussion) + ETH infrastructure
The EIP-4844 upgrade will introduce "proto-danksharding" and add the blob transaction type (EIP-4844) in the next Ethereum fork upgrade after The Merge, which is expected to improve the scalability of the 2nd layer Rollup while providing Pave the way for full sharding.
Added a new transaction type that includes additional storage - Blobs
Blobs start with only 128 KiB of storage
(1) A transaction contains at most 2 blobs, which is 256 KiB
(2) A Block contains up to 16, or 2 MiB; Target is 8, or 1 MiB (expandable)
Blob uses KZG Commitment Hash as Hash for data verification, similar to Merkle
After the node synchronizes the blob transaction on the chain, the blob part will be deleted after a period of time
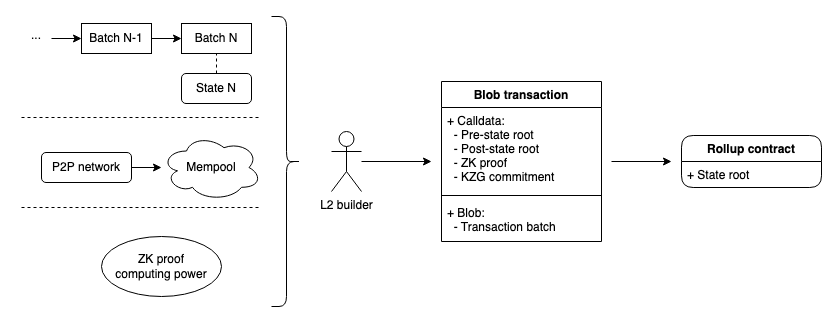
L2 needs to update the current contract in L1 to support DankSharding.
Celestia is implemented through fraud proofs. When the witness finds that the data has not been correctly deleted, the person will submit the fraud proof to alert other nodes. But there are minimum honesty assumptions (connecting to at least one honest node) and synchronization assumptions (when someone sends me a fraud proof, I need to ensure that I can be notified within a certain period of time).
After protoDanksharding, Ethereum and Polygon Avail adopt the method of KZG polynomial commitments (KZG commitments).
The KZG polynomial commitment scheme is theoretically superior to the fraud proof scheme, with smaller bandwidth requirements and less calculation required for sampling, and also eliminates the security assumptions in the fraud proof, including a few honest assumptions and synchronization assumptions. In the future, ETH also intends to introduce anti-post-quantum cryptography (refer to stark, which uses hash instead of using elliptic curve as the basis) to avoid quantum computer attacks.
2. Data structure optimization Verkle Tree
The concept of Verkle Tree was launched in 2018. As an important part of the ETH upgrade, compared with Merkle Tree, it has greatly improved the size of Proof; for data at the billion level, the proof of Merkle Tree is about Need 1kB, and for Verkle Tree, it will be less than 150Bytes.
Like Merkle Tree, Verkle Tree can also implement Proof of Inclusion (PoI), and only KZG root and Data can be verified without additional Proof, which saves bandwidth.
1. Requirements: Stateless Client
(1) The node does not store a complete State Tree, and only obtains the required State to verify the Block
(3) There are higher performance requirements for PoI of State Tree
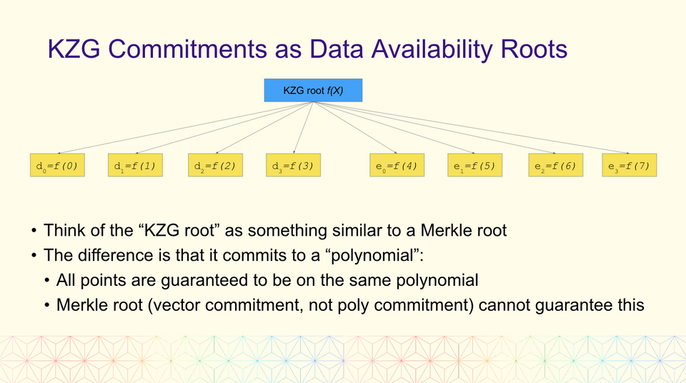
2. Review in Data AvailabilityKZG commitment
Each leaf is a point on the polynomial
constant size proof, has nothing to do with the number of leaf
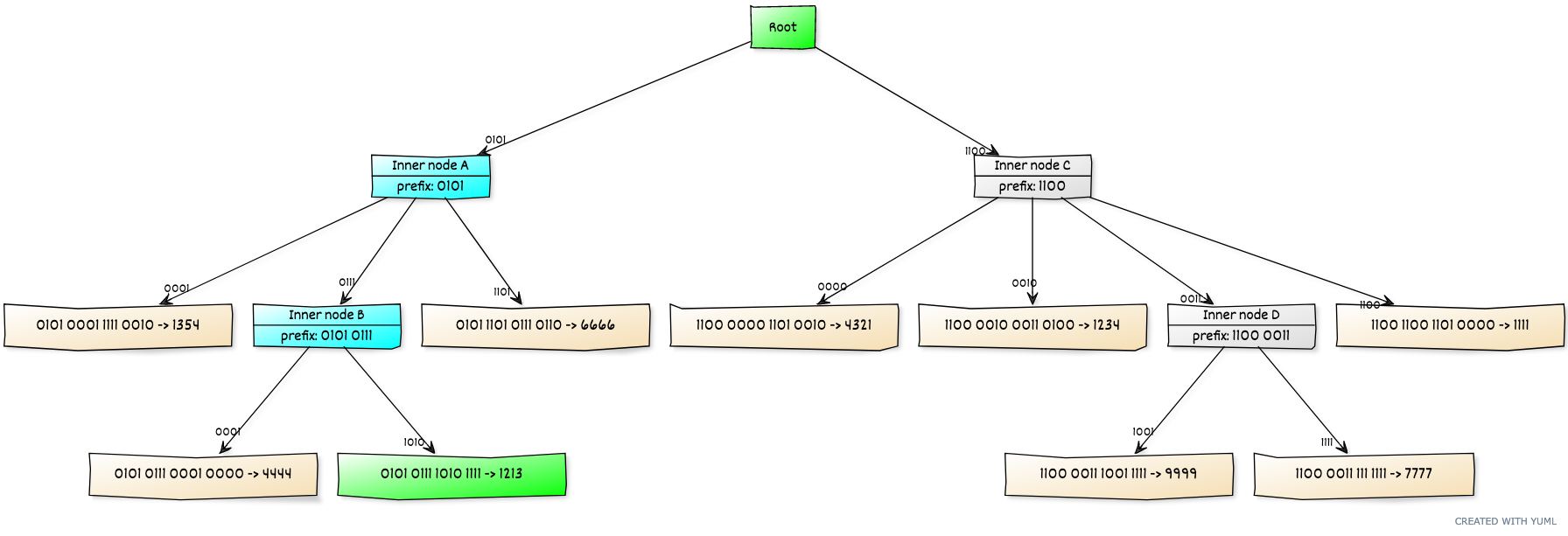
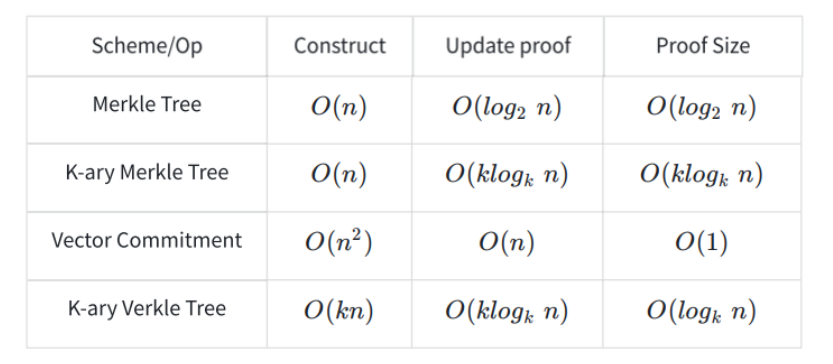
Building proofs in different tree structures, updating proofs, and the complexity required for proofs:

The Verkle scheme does not require the Ethereum client to download complete state data, making it possible for ETH validator light nodes (even supports mobile phone operation), polynomial commitment (the polynomial commitment scheme of the Verkle tree, KZG considered in the early stage, and IPA is still considered in the near future) ) needs to prove that the space complexity is greatly reduced, and the bandwidth requirement is also greatly reduced.
3. Zero-knowledge proof system
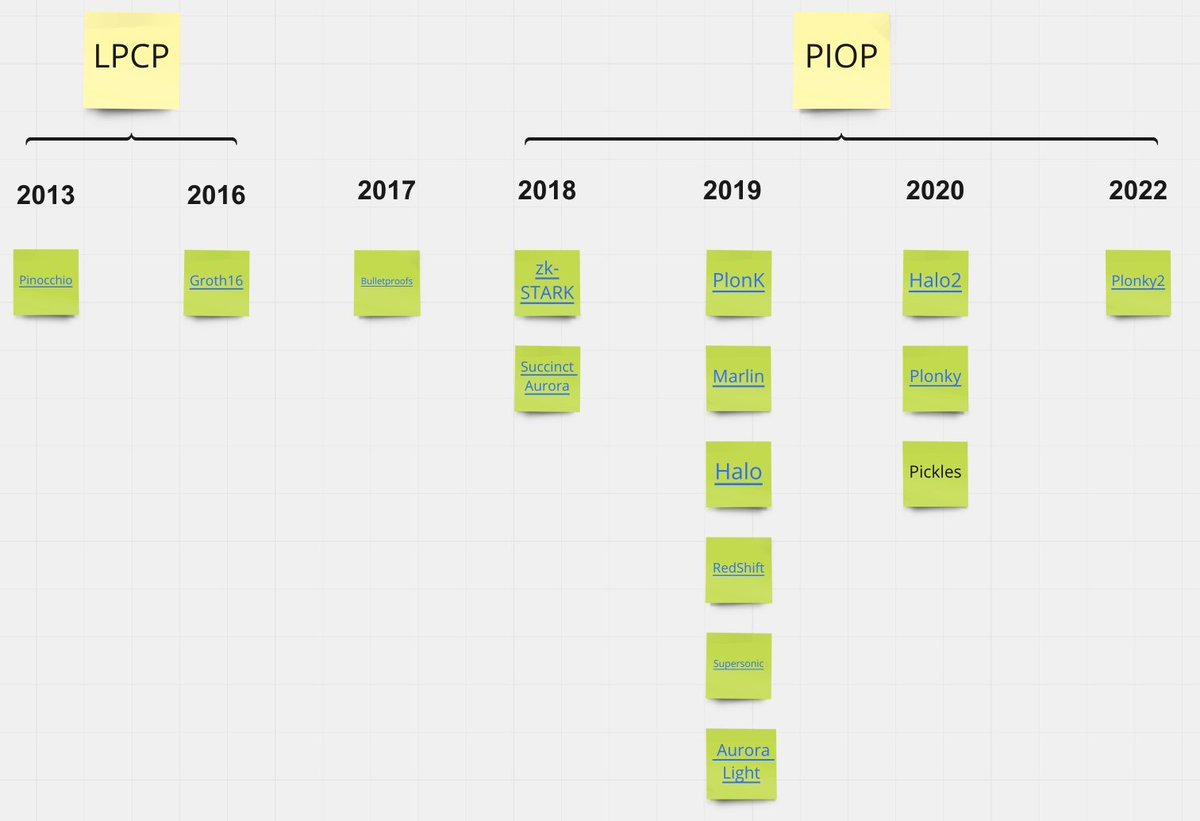
Early zk techniques (Groth16) belong to the linear PCP category. Besides requiring a trusted setup, the main disadvantage is that if a proof needs to be provided for a different calculation (different circuit/polynomial), a new setup is required. The recent zk technology PIOP class supports generic initial setup and transparent setup (no trust assumption required).
The new zk proof system can usually be described as PIOP (Polynomial Interactive Oracle Proof) + PCS (Polynomial Commitment Scheme). The former can be thought of as an agreed program used by the prover to convince the verifier, while the latter uses mathematical methods to ensure that the program cannot be broken. The project party can modify the PIOP as needed, and can choose among different PCS.
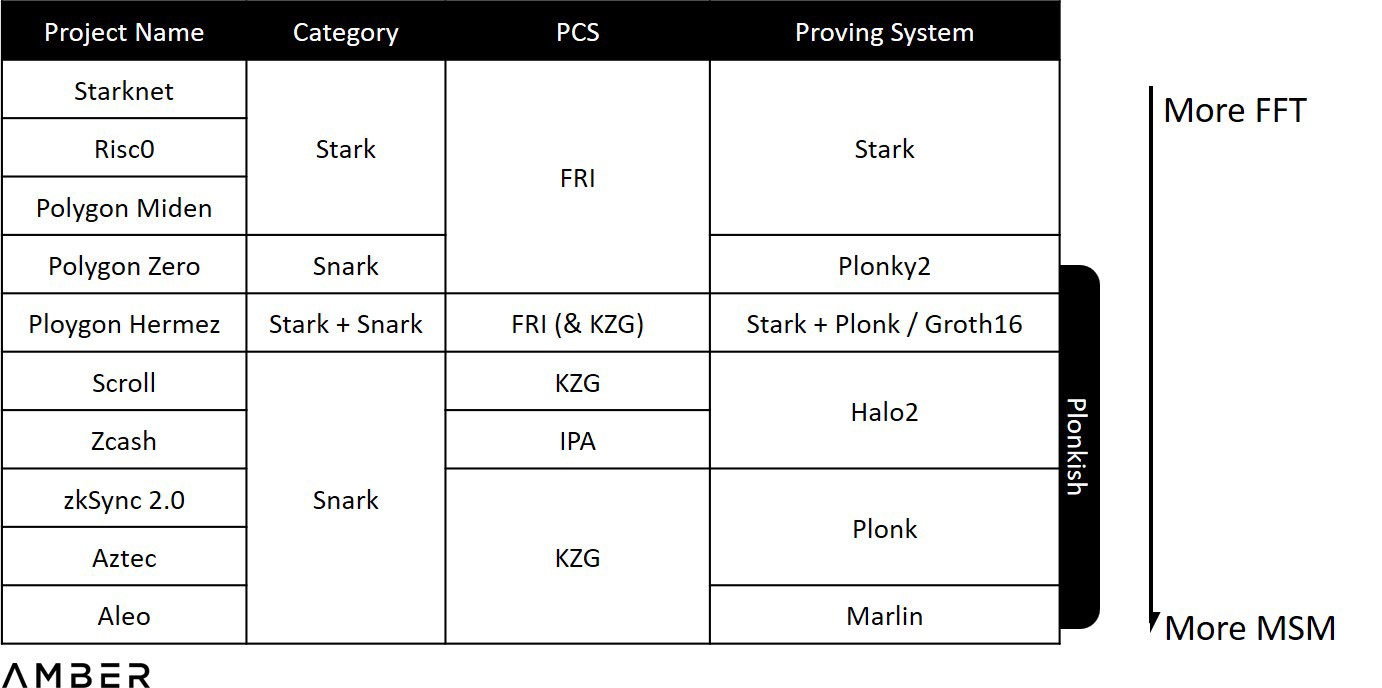
From the picture in Amber’s article, we can see that the most zk public chain projects adopt the KZG scheme, including Ploygon Hermez, Scoll, Zksync2.0, Aztec, Aleo, Manta, and PSE (Privacy and Exploration Team) supported by the Ethereum Foundation. The KZG scheme is also used. Starknet, Risc0, and Polygon Miden use the FRI scheme, and Polygon Zkvm (Hermez) is a combination of FRI and KZG.
It is worth mentioning that some new zero-knowledge proof systems support the switching of polynomial commitment schemes, and KZG can also switch to other polynomial commitment schemes in the future.
Original link