secondary title
1. The precision of floating-point arithmetic
At present, mainstream computer languages mostly follow the IEEE 754 standard for representing floating-point numbers, and the Rust language is no exception. The following is the description of the double-precision floating-point type f64 in the Rust language and the storage form of binary data in the computer:
picture
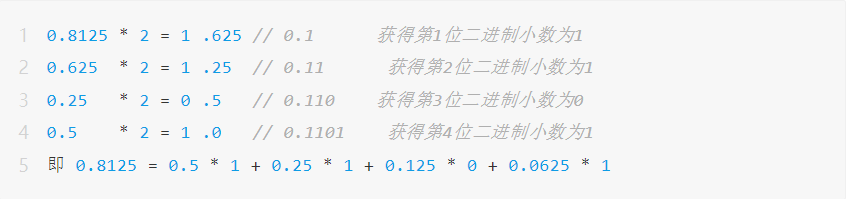
Floating-point numbers are expressed in scientific notation with a base of 2. For example, the binary number 0.1101 with a limited number of digits can be used to represent the decimal 0.8125. The specific conversion method is as follows:
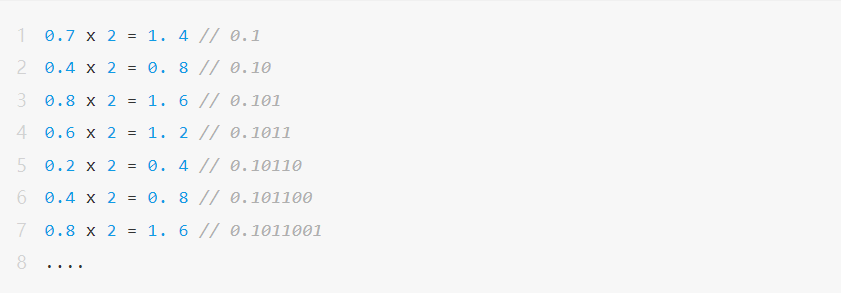
However, for another decimal 0.7, there will be the following problems in the process of actually converting it into a floating point number:
That is, the decimal 0.7 will be represented as 0.101100110011001100.....(infinite loop), which cannot be accurately represented by a floating-point number with a finite bit length, and there is a phenomenon of "rounding (Rounding)".

Assuming that on the NEAR public chain, 0.7 NEAR tokens need to be distributed to ten users, the specific number of NEAR tokens distributed to each user will be calculated and saved in the result_0 variable.

The output of executing this test case is as follows:
It can be seen that in the above floating-point calculation, the value of amount does not exactly represent 0.7, but a very approximate value of 0.69999999999999995559. Furthermore, for a single division operation such as amount/divisor, the operation result will also become an imprecise 0.069999999999999999, not the expected 0.07. This shows the uncertainty of floating-point arithmetic.
In this regard, we have to consider using other types of numerical representation methods in smart contracts, such as fixed-point numbers.
According to the fixed position of the decimal point of fixed-point numbers, there are two types of fixed-point numbers: fixed-point (pure) integers and fixed-point (pure) decimals.
If the decimal point is fixed after the lowest digit of the number, it is called a fixed-point integer
In actual smart contract writing, a fraction with a fixed denominator is usually used to represent a certain value, such as the fraction ' x/N ', where ' N ' is a constant and ' x ' can vary.

If the value of "N" is "1,000,000,000,000,000,000", that is: ' 10^18 ', then the decimal can be expressed as an integer, like this:
In NEAR Protocol, the common value of N is ' 10^24 ', that is, 10^24 yoctoNEAR is equivalent to 1 NEAR token.
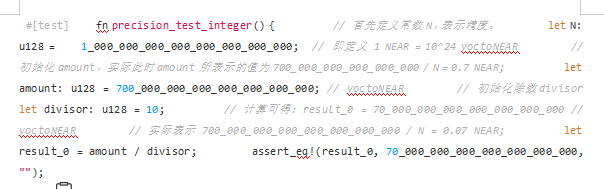
Based on this, we can modify the unit test in this section to calculate as follows:

In this way, the numerical actuarial calculation result can be obtained: 0.7 NEAR / 10 = 0.07 NEAR
2. Rust integer calculation accuracy problem
From the description in Section 1 above, it can be found that the use of integer operations can solve the problem of loss of precision in floating-point operations in certain operation scenarios.
However, this does not mean that the results of calculations using integers are completely accurate and reliable. This section describes some of the reasons that affect the precision of integer calculations.
2.1 Operation order
For multiplication and division with the same arithmetic priority, the change of the sequence may directly affect the calculation result, resulting in the problem of integer calculation accuracy.

For example, the following operations exist:

The results of executing unit tests are as follows:
We can find that result_0 = a * c / b and result_1 = (a / b) * c although their calculation formulas are the same, but the results are different.
The specific reason for the analysis is: For integer division, the precision less than the divisor will be discarded. Therefore, in the process of calculating result_1, the first calculated (a / b) will first lose the calculation precision and become 0; while in the calculation of result_0, the result of a * c will be calculated first 20_0000, which will be greater than the divisor b, so The problem of precision loss is avoided, and correct calculation results can be obtained.

2.2 Order of magnitude too small

The specific results of this unit test are as follows:
It can be seen that the equivalent result_0 and result_1 calculation results of the calculation process are not the same, and result_1 = 13 is closer to the actual expected calculation value: 13.3333....
3. How to write a numerical actuarial Rust smart contract
Ensuring the correct precision is very important in smart contracts. Although the Rust language also has the problem of loss of precision in the results of integer operations, we can take the following protective measures to improve the precision and achieve satisfactory results.
3.1 Adjust the operation order of the operation
Prefers integer multiplication over integer division.
3.2 Increasing the order of magnitude of integers
Integers use larger orders of magnitude, creating larger molecules.
For example, for a NEAR token, if you define N = 10 as described above, it means: if you need to express the NEAR value of 5.123, the integer value used in the actual operation will be expressed as 5.123* 10^10 = 51_230_000_000 . This value continues to participate in subsequent integer operations, which can improve the accuracy of operations.
3.3 Loss of accumulative operation precision
For integer calculation precision problems that cannot be avoided, the project party can consider recording the cumulative loss of calculation precision.

Assume the scenario of using fn distribute(amount: u128, offset: u128) -> u128 to distribute tokens to USER_NUM users as follows.
In this test case, the system will distribute 10 Tokens to 3 users each time. However, due to the precision of integer calculations, when calculating per_user_share in the first round, the integer calculation result obtained is 10 / 3 = 3, that is, users in the first round of distribute will receive 3 tokens on average, and a total of 9 tokens will be distributed.
At this point, it can be found that there is still one token in the system that has not been distributed to users. For this reason, it can be considered to temporarily save the remaining token in the system global variable offset. Waiting for the next time the system calls distribute to distribute tokens to users, this value will be taken out and tried to be distributed to users together with the amount of tokens distributed in this round.
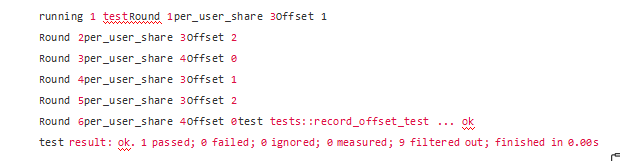
The simulated token distribution process is as follows:
It can be seen that when the system starts to distribute tokens in the third round, the accumulated offset value of the system has reached 2, and this value will be added together with the 10 tokens to be distributed in this round again and distributed to users. (There will be no precision loss in this calculation per_user_share = token_to_distribute / USER_NUM = 12 / 3 = 4.)
On the whole, in the first 3 rounds, the system issued a total of 30 Tokens. Each user has obtained 3, 3, and 4 tokens in each round. At this time, the user has also obtained a total of 30 tokens, which has achieved the system's goal of fully distributing bonuses.
3.4 Using the Rust Crate library rust-decimal
This Rust library is suitable for fractional financial calculations that require efficient precision calculations and no rounding errors.
3.5 Consider the rounding mechanism